
【题目】在平面直角坐标系xOy中,反比例数y=![]() 的图象过点A(6,1).
的图象过点A(6,1).
(1)求反比例数的表达式;
(2)过点A的直线与反比例数y=![]() 图象的另一个交点为B,与y轴交点交于点P.
图象的另一个交点为B,与y轴交点交于点P.
①若点P为原点,直接写出点B的坐标;
②若PA=2PB,求点P的坐标.
【答案】(1)y=![]() ;(2)①B点的坐标为(﹣6,﹣1);②P的坐标为(0,﹣1).
;(2)①B点的坐标为(﹣6,﹣1);②P的坐标为(0,﹣1).
【解析】
(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出m值,从而得出反比例函数表达式;
(2)①根据中心对称的性质即可求得;
②作AC⊥y轴于C,BD⊥y轴于D,通过证得△APC∽△BPD,得出![]() 2,求得B的横坐标坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令x=0,即可求得P的坐标.
2,求得B的横坐标坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令x=0,即可求得P的坐标.
(1)把(6,1)代入反比例函数解析式,得1![]() ,∴m=6;
,∴m=6;
(2)①由于直线过原点,该函数为正比例函数.
∵正比例函数和反比例函数图象都是关于原点中心对称的,∴两图象的交点关于原点成中心对称,∴点B、点A关于原点成中心对称.
∵A点的坐标为(6,1),∴B点的坐标为(﹣6,﹣1).
②作AC⊥y轴于C,BD⊥y轴于D.
∵AC∥BD,∴△APC∽△BPD,∴![]() .
.
∵AP=2PB,∴AC=2BD.
∵AC=6,∴BD=3,∴B的横坐标为﹣3,把x=﹣3代入y![]() 得y=﹣2,∴B(﹣3,﹣2),设直线AB的解析式为y=kx+b,把A(6,1),B(﹣3,﹣2)代入得
得y=﹣2,∴B(﹣3,﹣2),设直线AB的解析式为y=kx+b,把A(6,1),B(﹣3,﹣2)代入得![]() ,解得:
,解得: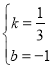 ,∴直线AB的解析式为y
,∴直线AB的解析式为y![]() x﹣1,令x=0,则y=﹣1,∴P的坐标为(0,﹣1).
x﹣1,令x=0,则y=﹣1,∴P的坐标为(0,﹣1).



科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
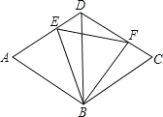
【题目】如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是( )
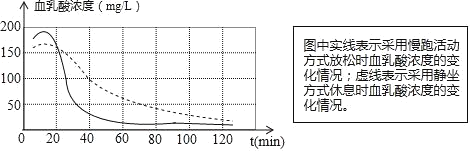
A. 运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B. 运动员高强度运动后,最高血乳酸浓度大约为250mg/L
C. 采用慢跑活动方式放松时,运动员必须慢跑70min后才能基本消除疲芳
D. 运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a2b+c>0;④a+c>0,其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
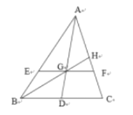
【题目】如图,已知在△ABC中,点D为BC边上一点(不与点B,点C重合),连结AD,点E、点F分别为AB、AC上的点,且EF∥BC,交AD于点G,连结BG,并延长BG交AC于点H.已知![]() =2,①若AD为BC边上的中线,
=2,①若AD为BC边上的中线,![]() 的值为
的值为![]() ;②若BH⊥AC,当BC>2CD时,
;②若BH⊥AC,当BC>2CD时,![]() <2sin∠DAC.则( )
<2sin∠DAC.则( )
A. ①正确;②不正确B. ①正确;②正确
C. ①不正确;②正确D. ①不正确;②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
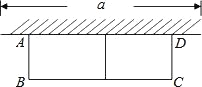
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com