
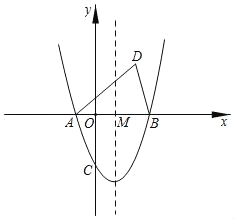
【题目】如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0)、B两点,与y轴交于点C(0,﹣3).
(1)求抛物线的函数解析式;
(2)已知点P(m,n)在抛物线上,当﹣2≤m<3时,直接写n的取值范围;
(3)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线上是否存在点P,使△ABP与△ABD全等?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)﹣4≤n≤5;(3)P的坐标为(0,﹣3)或(2,﹣3).
【解析】
(1)将A,C两点的坐标代入解析式可得抛物线的解析式;
(2)根据二次函数的性质可求n的取值范围;
(3)在x轴上方的P不存在,点P只可能在x轴的下方,按照题意,分别求解即可.
解:(1)将点C坐标代入函数表达式得:y=x2+bx﹣3,
将点A的坐标代入上式并解得:b=﹣2,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)令y=x2﹣2x﹣3=0,则x=3或﹣1,即点B(3,0),
函数的对称轴为x=1,
m=﹣2时,n=4+4﹣3=5,
m<3,函数的最小值为顶点纵坐标的值:﹣4,
故﹣4≤n≤5;
(3)点D与点C(0,﹣3)关于点M对称,则点D(2,3),
在x轴上方的P不存在,点P只可能在x轴的下方,
如下图当点P在对称轴右侧时,点P为点D关于x轴的对称点,此时△ABP与△ABD全等,
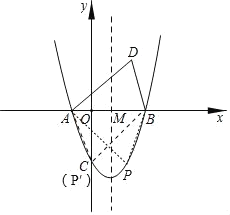
即点P(2,﹣3);
同理点C(P′)也满足△ABP′与△ABD全等,
即点P′(0,﹣3);
故点P的坐标为(0,﹣3)或(2,﹣3).


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(﹣3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.
(1)求抛物线的解析式;
(2)连接BE,求h为何值时,△BDE的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
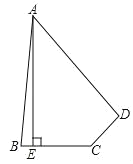
【题目】如图,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=17,BC=8,CD=6,则四边形ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个大小一样的正六边形,可按下列方式进行拼接:
方式1:如图1;
方式2:如图2;
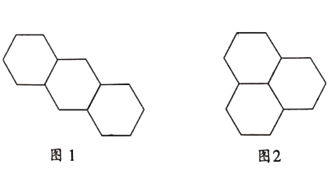
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是_______.有![]() 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则
个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
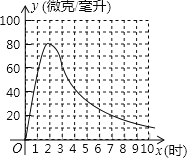
【题目】某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约多少小时,每毫升血液中含药量最大,最大值是多少微克;
(2)服药后,药物发挥作用的时间大约有多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,连结AD,点E是AD的中点,连结BE并延长交CD于F点.
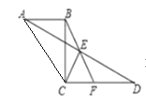
(1)请说明△ABE≌△DFE的理由;
(2)连结CE,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径AB、CD相互垂直,P为弧BC上任意一点,连PC、PA、PD、PB,下列结论:①∠APC=∠DPE;②∠AED=∠DFA;③![]() ;其中正确的是( )
;其中正确的是( )
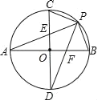
A. ①③B. 只有①C. 只有②D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com