
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌгы
ЃЌгы![]() жсЕФСэвЛИіНЛЕуЮЊЕу
жсЕФСэвЛИіНЛЕуЮЊЕу![]() .
.
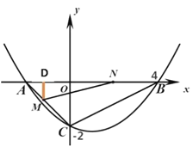
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЭЌЪБЕу
дЫЖЏЃЌЫйЖШЮЊ1ИіЕЅЮЛГЄЖШ/УыЃЌЭЌЪБЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌби
ГіЗЂЃЌби![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЫйЖШЮЊ2ИіЕЅЮЛГЄЖШ/УыЃЌЕБЕу
дЫЖЏЃЌЫйЖШЮЊ2ИіЕЅЮЛГЄЖШ/УыЃЌЕБЕу![]() ЁЂ
ЁЂ![]() гавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЌСЌНг
гавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЌСЌНг![]() ЃЌЩшдЫЖЏЪБМфЮЊ
ЃЌЩшдЫЖЏЪБМфЮЊ![]() УыЃЌЕБ
УыЃЌЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЕФУцЛ§
ЕФУцЛ§![]() зюДѓЃЌВЂЧѓГі
зюДѓЃЌВЂЧѓГі![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕу![]() дк
дк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() дкХзЮяЯпЩЯЃЌЪЧЗёДцдкЕу
дкХзЮяЯпЩЯЃЌЪЧЗёДцдкЕу![]() ЁЂ
ЁЂ![]() ЃЌЪЙЕУвдЕу
ЃЌЪЙЕУвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу![]() зјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
зјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕБ
ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() зюДѓжЕЮЊ
зюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉДцдкТњзуЬѕМўЕФЕу
ЃЛЃЈ3ЃЉДцдкТњзуЬѕМўЕФЕу![]() га4ИіЃЌЗжБ№ЪЧ
га4ИіЃЌЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУaЁЂbЁЂcЕФжЕЃЌМДПЩЧѓЕУХзЮяЯпНтЮіЪН.
ЃЈ2ЃЉРћгУЖдГЦжсКЭBЕузјБъЃЌЧѓЕУAЕузјБъЃЈ-2,0ЃЉЃЌЫљвд![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌЙ§Еу
ЪЧЕШбќжБНЧШ§НЧаЮЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() .ЩшЕуNЕФдЫЖЏЪБМфЮЊtЃЌгУКЌtЕФДњЪ§ЪНЗжБ№БэЪОANЁЂAMЃЌ
.ЩшЕуNЕФдЫЖЏЪБМфЮЊtЃЌгУКЌtЕФДњЪ§ЪНЗжБ№БэЪОANЁЂAMЃЌ![]() ЃЛ
ЃЛ![]() ЃЌДњШыПЩЕУЙигкtЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌРћгУЖЅЕуЪНЃЌЧѓЕУзюжЕМДПЩ.
ЃЌДњШыПЩЕУЙигкtЕФЖўДЮКЏЪ§ЙиЯЕЪНЃЌРћгУЖЅЕуЪНЃЌЧѓЕУзюжЕМДПЩ.
ЃЈ3ЃЉЗжЧщПіЬжТлЃКРћгУЦНааЯпЫФБпаЮаджЪЃЌШ§НЧаЮЯрЫЦМДПЩЕУГі.
ЃЈ1ЃЉНтЃКвРЬтвтЕУ
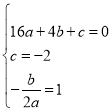 ЃЌНтЕУЃК
ЃЌНтЕУЃК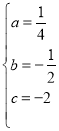 ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊЃК
ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() .
.
ЃЈ2ЃЉЁпЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ![]() .
.
Ёр![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБЕу![]() дЫЖЏ
дЫЖЏ![]() УыЪБЃЌ
УыЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Й§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() .
.
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
Ёр![]() .
.
гжЁп![]() ЃЌЁр
ЃЌЁр![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ
ЕБЕу![]() дЫЖЏ
дЫЖЏ![]() УыЪБЃЌ
УыЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() зюДѓжЕЮЊ
зюДѓжЕЮЊ![]() .
.
ЃЈ3ЃЉДцдкТњзуЬѕМўЕФЕу![]() га4ИіЃЌЗжБ№ЪЧ
га4ИіЃЌЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
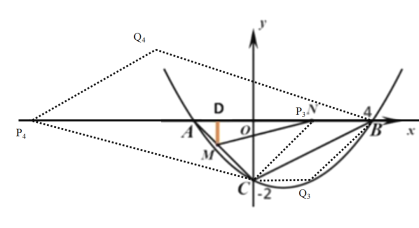



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊx1ЃЌx2ЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬ4kx2Љ4kx+k+1=0ЕФСНИіЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЪЧЗёДцдкЪЕЪ§kЃЌЪЙЃЈ2x1Љx2ЃЉЃЈx1Љ2x2ЃЉ=Љ![]() ГЩСЂЃПШєДцдкЃЌЧѓГіkЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ГЩСЂЃПШєДцдкЃЌЧѓГіkЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧѓЪЙ![]() Љ2ЕФжЕЮЊећЪ§ЕФЪЕЪ§kЕФећЪ§жЕЃЛ
Љ2ЕФжЕЮЊећЪ§ЕФЪЕЪ§kЕФећЪ§жЕЃЛ
ЃЈ3ЃЉШєk=Љ2ЃЌІЫ=![]() ЃЌЪдЧѓІЫЕФжЕЃЎ
ЃЌЪдЧѓІЫЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
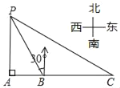
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГКЃЕСДЌвд20КЃРя/аЁЪБЕФЫйЖШдкФГКЃгђжДаабВКНШЮЮёЃЌЕБКЃМрДЌгЩЮїЯђЖЋКНаажСAДІЪЙЃЌВтЕУЕКгьPЧЁКУдкЦфе§ББЗНЯђЃЌМЬајЯђЖЋКНаа1аЁЪБЕНДяBДІЃЌВтЕУЕКгьPдкЦфББЦЋЮї30ЁуЗНЯђЃЌБЃГжКНЯђВЛБфгжКНаа2аЁЪБЕНДяCДІЃЌЧѓГіДЫЪБКЃМрДЌгыЕКгьPжЎМфЕФОрРыЃЈМДPCЕФГЄЃЌНсЙћОЋШЗЕН0.1ЃЉЃЈВЮПМЪ§ОнЃК![]() Ёж1.732ЃЌ
Ёж1.732ЃЌ![]() Ёж1.414ЃЉ
Ёж1.414ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
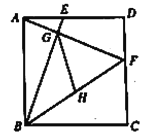
ЁОЬтФПЁПвбжЊе§ЗНаЮ![]() ЕФБпГЄЮЊ6ЃЌЕу
ЕФБпГЄЮЊ6ЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дк
ЗжБ№дк![]() ЃЌ
ЃЌ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ______.
ЕФГЄЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ![]() ЃЌЯТСаНсТлЃКЂй
ЃЌЯТСаНсТлЃКЂй![]() ЃЛЂк9a+3b+c=0ЃЛЂлШєЕу
ЃЛЂк9a+3b+c=0ЃЛЂлШєЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧДЫКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђ
ЪЧДЫКЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌдђ![]() ЃЛЂм
ЃЛЂм![]() .Цфжае§ШЗЕФИіЪ§ЃЈ ЃЉ
.Цфжае§ШЗЕФИіЪ§ЃЈ ЃЉ
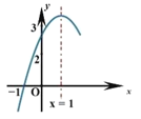
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+6ОЙ§ЕуAЃЈЉ3ЃЌ0ЃЉКЭЕуBЃЈ2ЃЌ0ЃЉЃЎжБЯпy=hЃЈhЮЊГЃЪ§ЃЌЧв0ЃМhЃМ6ЃЉгыBCНЛгкЕуDЃЌгыyжсНЛгкЕуEЃЌгыACНЛгкЕуFЃЌгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгBEЃЌЧѓhЮЊКЮжЕЪБЃЌЁїBDEЕФУцЛ§зюДѓЃЛ
ЃЈ3ЃЉвбжЊвЛЖЈЕуMЃЈЉ2ЃЌ0ЃЉЃЎЮЪЃКЪЧЗёДцдкетбљЕФжБЯпy=hЃЌЪЙЁїOMFЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіhЕФжЕКЭЕуGЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШчЭМЃЌХзЮяЯпyЃНax2ЃЋ3axЃЋcЃЈaЃО0ЃЉгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЕуAдкЕуBзѓВрЃЌЕуBЕФзјБъЮЊ(1ЃЌ0)ЃЌC(0ЃЌЃ3)
(1) ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2) ШєЕуDЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЧѓЫФБпаЮABCDУцЛ§ЕФзюДѓжЕ.
(3) ШєЕуEдкxжсЩЯЃЌЕуPдкХзЮяЯпЩЯЃЌЪЧЗёДцдквдAЁЂCЁЂEЁЂPЮЊЖЅЕуЧввдACЮЊвЛБпЕФЦНааЫФБпаЮЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдкБп
ЃЌдкБп![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЯпЖЮ
ЗжБ№ЪЧЯпЖЮ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() КЭ
КЭ![]() ЃЌзї
ЃЌзї![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌШчЭМ1ЫљЪО.
ЃЌШчЭМ1ЫљЪО.

ЃЈ1ЃЉЧыХаЖЯЫФБпаЮ![]() ЪЧЪВУДЬиЪтЕФЫФБпаЮЃЌВЂжЄУїФуЕФНсТлЃЛ
ЪЧЪВУДЬиЪтЕФЫФБпаЮЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊЕН
ЫГЪБеыа§зЊЕН![]() ЃЌНЛЯпЖЮ
ЃЌНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌШчЭМ2ЫљЪОЃЌЧыжЄУїЃК
ЃЌШчЭМ2ЫљЪОЃЌЧыжЄУїЃК![]() ЃЛ
ЃЛ
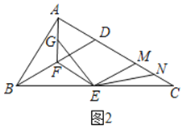
ЃЈ3ЃЉдкЕкЃЈ2ЃЉЬѕМўЯТЃЌШєЕу![]() ЪЧ
ЪЧ![]() жаЕуЃЌЧв
жаЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌШчЭМ3ЃЌЧѓ
ЃЌШчЭМ3ЃЌЧѓ![]() ЕФГЄЖШ.
ЕФГЄЖШ.
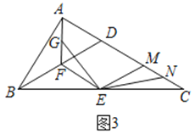
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
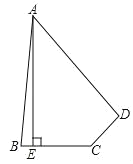
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌЁЯABC+ЁЯADCЃН180ЁуЃЌABЃНADЃЌAEЁЭBCгкЕуEЃЌШєAEЃН17ЃЌBCЃН8ЃЌCDЃН6ЃЌдђЫФБпаЮABCDЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com