
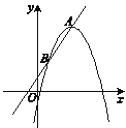
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��������W����A��B���㣬���е�A��������W�Ķ��㣮����A��ֱ��
��������W����A��B���㣬���е�A��������W�Ķ��㣮����A��ֱ��![]() ���˶�ʱ��������W���A��ƽ���˶�����������ƽ�ƵĹ����У��߶�AB�ij��ȱ��ֲ��䣮
���˶�ʱ��������W���A��ƽ���˶�����������ƽ�ƵĹ����У��߶�AB�ij��ȱ��ֲ��䣮
Ӧ������Ľ��ۣ�����������⣺
��ƽ��ֱ������ϵxOy�У���ֱ֪��![]() ����A��ֱ��
����A��ֱ��![]() �ϵ�һ�����㣬�ҵ�A�ĺ�����Ϊ
�ϵ�һ�����㣬�ҵ�A�ĺ�����Ϊ![]() ����AΪ�����������
����AΪ�����������![]() ��ֱ��
��ֱ��![]() ����һ������Ϊ��B��
����һ������Ϊ��B��
��1����![]() ʱ����������
ʱ����������![]() �Ľ���ʽ��AB�ij���
�Ľ���ʽ��AB�ij���
��2������B��ֱ��OA�ľ���ﵽ���ʱ��ֱ��д����ʱ��A�����ꣻ
��3������A����ֱ��![]() ���ֱ�߽�ֱ��
���ֱ�߽�ֱ��![]() �ڵ�C����CΪ�����������
�ڵ�C����CΪ�����������![]() ��ֱ��
��ֱ��![]() ����һ������Ϊ��D��
����һ������Ϊ��D��
�ٵ�AC��BDʱ����![]() ��ֵ��
��ֵ��
������A��B��C��DΪ���㹹�ɵ�ͼ�����ı��Σ������ڽǶ�����С��180����ʱ��ֱ��д������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��![]() ��
��
��������
��1������t=0ʱ��A�������������ǣ�0��-2�������ô���ϵ����������������ߵĽ���ʽ����B�����������ã�
��2����OAB�����һ������OA��Сʱ��B��OA�ľ��뼴��OAB��OA���ϵĸ����ʱOA��AB���ݴ˼�����⣻
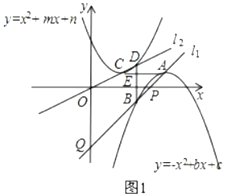
��3���ٷ���һ����AC��BD���ڵ�E��ֱ��l1��y=x-2����x�ᡢy�ύ�ڵ�P��Q����ͼ1�����ɵ�D��������C2��y=[x-��2t-4��]2+��t-2���ϣ��ɵ�![]() =[��t-1��-��2t-4��]2+��t-2�����ⷽ�̼��ɵõ�t��ֵ��
=[��t-1��-��2t-4��]2+��t-2�����ⷽ�̼��ɵõ�t��ֵ��
����������ֱ��l1��y=x-2��x�ύ�ڵ�P������A��y���ƽ���ߣ�����B��x���ƽ���ߣ����ڵ�N������ͼ2��������BD��AC���ɵ�t-1=2t-![]() ���ⷽ�̼��ɵõ�t��ֵ��
���ⷽ�̼��ɵõ�t��ֵ��
����ֱ��l1��l2���ڵ�M�����ŵ�A���������˶����ӵ�D���M�غϣ�����B���M�غϵĹ����У��ɵ�����������t��ȡֵ��Χ��
�⣺��1���ߵ�A��ֱ��l1��y=x-2�ϣ��ҵ�A�ĺ�����Ϊ0��
���A��������0��-2����
��������C1�Ľ���ʽΪy=-x2-2��
�ߵ�B��ֱ��l1��y=x-2�ϣ�
���B��������x��x-2����
�ߵ�B��������C1��y=-x2-2�ϣ�
��x-2=-x2-2��
���x=0��x=-1��
�ߵ�A���B���غϣ�
���B��������-1��-3����
���ɹ��ɶ�����AB=![]() ��
��
��2����OA��ABʱ����B��ֱ��OA�ľ���ﵽ�����OA�Ľ���ʽ��y=-x����![]() ����ã�
����ã�![]() ��
��
���A��������1��-1����
��3���ٷ���һ����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ����
����![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����ͼ1����
����ͼ1����
���![]() �͵�
�͵�![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() �ᣬ
�ᣬ
��![]() �ᣮ
�ᣮ
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
�ߵ�![]() ��ֱ��
��ֱ��![]() �ϣ��ҵ�
�ϣ��ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
���![]() ������Ϊ
������Ϊ![]() ��
��
���![]() ������Ϊ
������Ϊ![]() ��
��
��![]() �ᣬ
�ᣬ
���![]() ��������Ϊ
��������Ϊ![]() ��
��
�ߵ�![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
���![]() ������Ϊ
������Ϊ![]() ��
��
��������![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() ��
��
���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
�ߵ�![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
���![]() ������Ϊ
������Ϊ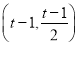 ��
��
�ߵ�![]() ��������
��������![]() �ϣ�
�ϣ�
��![]() ��
��
���![]() ��
��![]() ��
��
�ߵ�![]() ʱ����
ʱ����![]() ���
���![]() �غϣ�
�غϣ�
��![]()
����������ֱ��l1��y=x-2��x�ύ�ڵ�P������A��y���ƽ���ߣ�����B��x���ƽ���ߣ����ڵ�N������ͼ2��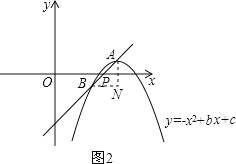
���ANB=90������ABN=��OPB��
����ABN��BN=ABcos��ABN��AN=ABsin��ABN��
����������C1�涥��Aƽ�ƵĹ����У�
AB�ij��Ȳ��䣬��ABN�Ĵ�С���䣬
��BN��AN�ij���Ҳ���䣬����A���B�ĺ�����IJ��Լ�������IJ���ֲ��䣮
ͬ������C���D�ĺ�����IJ��Լ�������IJ�Ҳ���ֲ��䣮
�ɣ�1��֪����A������Ϊ��0��-2��ʱ����B������Ϊ��-1��-3����
�൱��A������Ϊ��t��t-2��ʱ����B������Ϊ��t-1��t-3����
��AC��x�ᣬ
���C��������Ϊt-2��
�ߵ�C��ֱ��l2��y��![]() x�ϣ�
x�ϣ�
���C��������2t-4��t-2����
��t=2�����C��������0��0����
��������C2�Ľ���ʽΪy=x2��
�ߵ�D��ֱ��l2��y��![]() x�ϣ�
x�ϣ�
�����D������Ϊ(x��![]() )��
)��
�ߵ�D��������C2��y=x2�ϣ�
��![]() ��x2��
��x2��
���x��![]() ��x=0��
��x=0��
�ߵ�C���D���غϣ�
���D������Ϊ(![]() ��
��![]() )��
)��
�൱��C������Ϊ��0��0��ʱ����D������Ϊ(![]() ��
��![]() )��
)��
�൱��C������Ϊ��2t-4��t-2��ʱ����D������Ϊ(2t![]() ��t
��t![]() )��
)��
��BD��AC��
��t1��2t![]() ��
��
��t��![]() ��
��
��t��ȡֵ��Χ��t��![]() ��t��5��
��t��5��
��ֱ��l1��l2���ڵ�M�����ŵ�A���������˶����ӵ�D���M�غϣ�����B���M�غϵĹ����У���A��B��C��DΪ���㹹�ɵ�ͼ�β����ı��Σ�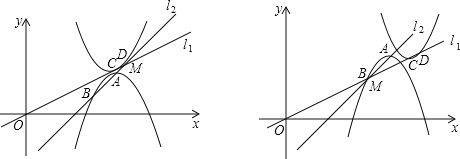



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����![]() �ͺ���
�ͺ���![]() (m�dz�������
(m�dz�������![]() )��ͼ�������( )
)��ͼ�������( )
A. 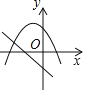 B.
B. 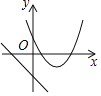
C. 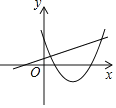 D.
D. 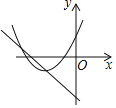
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʵ����ʾ������y=|a��x��1��2��1|��ͼ��ԭ�㣬С��ͬѧ�о��ó�������ۣ�
��a=1����������y��x���������С����x��ȡֵ��Χһ����x��0��
��������|a��x��1��2��1|=k������ʵ���⣬��k��ȡֵ��Χ��k��1��
����M��m1��n����N��m2��n����P��m3��n����Q��m4��n����n��0������������ͼ����ĸ���ͬ�㣬��m1��m2��m3��m4������m2+m3��m1=m4��������ȷ�Ľ����У�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����صƵĵ���![]() ��ֱ��ˮƽ����
��ֱ��ˮƽ����![]() ���߶�Ϊ1.6�ף�֧�ܲ��ֵ���״Ϊ�������µ������ߣ��䶥��
���߶�Ϊ1.6�ף�֧�ܲ��ֵ���״Ϊ�������µ������ߣ��䶥��![]() �����
�����![]() ��ˮƽ����Ϊ0.8�ף������ĸ߶�Ϊ2.4�ף�����
��ˮƽ����Ϊ0.8�ף������ĸ߶�Ϊ2.4�ף�����![]() �����
�����![]() ��ˮƽ����Ϊ1.4�ף�����ֶ���D�����ĸ߶�Ϊ______�ף�
��ˮƽ����Ϊ1.4�ף�����ֶ���D�����ĸ߶�Ϊ______�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʻ��������ͨ�¹ʵ���Ҫԭ������ĩ��С������λͬѧ�������Լ���ѧ��֪ʶ���٣���ͼ���۲�����ڵ��سdz��ϴ���ľ���Ϊ![]() �ĵ�
�ĵ�![]() ������ʱ��һ�����������������ʻ����ô˳���
������ʱ��һ�����������������ʻ����ô˳���![]() ����ʻ��
����ʻ��![]() �����õ�ʱ��Ϊ
�����õ�ʱ��Ϊ![]() �룬��
�룬��![]() ��
��![]() ��
��

![]() ��
��![]() ��
��![]() ֮���·�̣�
֮���·�̣�
![]() ���жϴ˳���Ƿ��˳��ϴ��ÿСʱ
���жϴ˳���Ƿ��˳��ϴ��ÿСʱ![]() ǧ�������ٶȣ�
ǧ�������ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�������ͼ��ʹ���̶ȵ�ֱ�߰�Ҫ��ͼ��
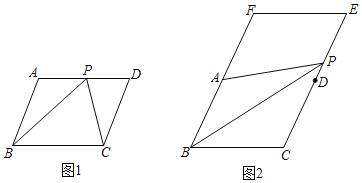
��1����ͼ1�У���P��ABCD��AD�ϵ��е㣬����P��һ���߶�PM��ʹPM��![]() AB��
AB��
��2����ͼ2�У���A��D�ֱ���BCEF��FB��EC�ϵ��е㣬�ҵ�P�DZ�EC�ϵĶ��㣬������PAB��һ����λ�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC�ǡ�O��ֱ������BD��AO��E������BC������O��OF��BC��F����BD=8cm��AE=2cm����OF�ij����ǣ�������

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��������ABCD�ı߳�Ϊ2����E��BC����һ�㣬��ABΪֱ����������������Բ
O������DCE��DE���ۣ���C�պ����ڰ�ԲO�ĵ�F������CE�ij�Ϊ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
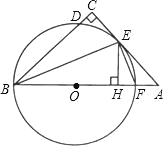
����Ŀ����ͼ������ABC�У���C=90������ABC��ƽ���߽�AC�ڵ�E������E��BE�Ĵ��߽�AB�ڵ�F����O����BEF�����Բ��
��1����֤��AC����O�����ߣ�
��2������E��EH��AB������ΪH����֤��CD=HF��
��3����CD=1��EH=3����BF��AF����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com