

分析 (1)直接根据速度和时间表示BP=t,CQ=2t;
(2)当点P与点Q相遇时,即P与Q重合,则两个动点的路程和为BC的长,即t+2t=8,求出即可;
(3)分两种情况:①P与Q相遇之前时,当0<t<$\frac{8}{3}$时,如图1,②P与Q相遇之前时,当$\frac{8}{3}$<t<4时,如图2,分别求PQ的长,代入面积公式计算即可.
解答 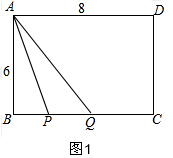 解:(1)由题意得:BP=t,CQ=2t;
解:(1)由题意得:BP=t,CQ=2t;
(2)t+2t=8,
t=$\frac{8}{3}$,
答:当t为$\frac{8}{3}$时,点P与点Q相遇;
(3)分两种情况:
①当0<t<$\frac{8}{3}$时,如图1,PQ=8-t-2t=8-3t,
S△APQ=$\frac{1}{2}$PQ•AB=6,
$\frac{1}{2}$(8-3t)×6=6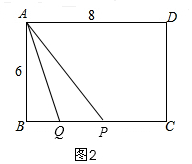 ,
,
t=2;
②当$\frac{8}{3}$<t<4时,如图2,PQ=QC-PC=2t-(8-t)=3t-8,
∴S△APQ=$\frac{1}{2}$PQ•AB=6,
$\frac{1}{2}$(3t-8)×6=6,
t=$\frac{10}{3}$;
综上所述,当t为2或$\frac{10}{3}$时,三角形APQ的面积为6cm2.
点评 本题主要考查了列一元一次方程来解决现实生活中的动点运动问题;解题的关键是准确表示出PB、CQ关于时间t的代数式,再根据等量关系列出方程来求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD为平行四边形,DF交AC的延长线于F点,AC=2CF,BE∥AC,BE与DF的延长线交于E点.则AF:BE的值为( )
如图,四边形ABCD为平行四边形,DF交AC的延长线于F点,AC=2CF,BE∥AC,BE与DF的延长线交于E点.则AF:BE的值为( )| A. | 2:3 | B. | 3:4 | C. | 4:5 | D. | 5:6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
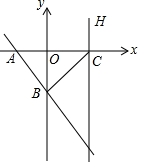 如图,在平面直角坐标系中,直线l与x轴交于点A(-1,0),与y轴交于点B(0,-2),点C是x轴上一点,且满足CA=CB
如图,在平面直角坐标系中,直线l与x轴交于点A(-1,0),与y轴交于点B(0,-2),点C是x轴上一点,且满足CA=CB查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=ax2+bx+c(a,b,c是常数) | B. | y=$\sqrt{{x}^{2}+1}$ | ||
| C. | y=(x+1)2-(x+1)(x-1) | D. | y=x2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com