
【题目】课上老师呈现一个问题:

下面提供三种思路:
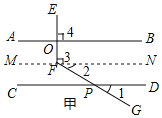
思路一:过点F作MN∥CD(如图甲);
思路二:过P作PN∥EF,交AB于点N;
思路三:过O作ON∥FG,交CD于点N.
解答下列问题:

(1)根据思路一(图甲),可求得∠EFG的度数为 ;
(2)根据思路二、三分别在图乙和图丙中作出符合要求的辅助线;
(3)请你从思路二、思路三中任选其中一种,写出求∠EFG度数的解答过程.
【答案】(1)120°;(2)见解析;(3)若选思路二,EFG=120°,解答过程见解析,若选思路三,EFG=120°,解答过程见解析.
【解析】
(1)如图甲(见解析),根据“两直线平行,同位角相等”,可得![]() 和
和![]() 的度数,从而可得
的度数,从而可得![]() 的度数;
的度数;
(2)利用直尺和直角三角板,通过“一放、二靠、三移、四画”的步骤即可画出;
(3)思路二:如图乙(见解析),先利用两次“两直线平行,内错角相等”求出![]() ,从而可得
,从而可得![]() ,再利用“两直线平行,同位角相等”即可得;思路三:如图丙(见解析),先利用两次“两直线平行,内错角相等”求出
,再利用“两直线平行,同位角相等”即可得;思路三:如图丙(见解析),先利用两次“两直线平行,内错角相等”求出![]() ,从而可得
,从而可得![]() ,再利用“两直线平行,同位角相等”即可得.
,再利用“两直线平行,同位角相等”即可得.
(1)如图甲,过F作![]()
![]()
![]() (两直线平行,同位角相等)
(两直线平行,同位角相等)
![]()
![]()
![]() ,即
,即![]()
![]() (两直线平行,同位角相等)
(两直线平行,同位角相等)
![]()
故答案为:![]() ;
;
(2)思路二:利用直尺和直角三角板,通过“一放、二靠、三移、四画”的步骤,过P作![]() ,具体如下:
,具体如下:
一放:放直角三角板,把直角三角板的一条直角边与直线EF重合
二靠:靠直尺,把直尺靠在直角三角板另一条直角边上
三移:直尺固定不动,移动直角三角板使其边与点P重合
四画:沿着直角三角板边画直线
思路三:按思路二同样的方法即可作出符合要求的辅助线
思路二(图乙)、思路三(图丙)的作图结果如下:

(3)若选思路二,解答过程如下:
如图乙,过P作![]()
![]() ,即
,即![]()
![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
![]()
![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
又![]()
![]()
![]()
![]() ;(两直线平行,同位角相等)
;(两直线平行,同位角相等)
若选思路三,解答过程如下:
如图丙,过O作![]()
![]()
![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
![]()
![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
又![]() ,即
,即![]()
![]()
![]()
![]() .(两直线平行,同位角相等)
.(两直线平行,同位角相等)


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,并过点
,并过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .抛物线
.抛物线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,四边形
,四边形![]() 的面积是
的面积是![]() .
.
![]() 求反比例函数、二次函数的解析式及抛物线的对称轴;
求反比例函数、二次函数的解析式及抛物线的对称轴;
![]() 如图
如图![]() ,点
,点![]() 从
从![]() 点出发以每秒
点出发以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向
向![]() 点运动,点
点运动,点![]() 从
从![]() 点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为
点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为等腰梯形;
为等腰梯形;
②设![]() 与对称轴的交点为
与对称轴的交点为![]() ,过
,过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于时间
关于时间![]() 的函数解析式,并指出
的函数解析式,并指出![]() 的取值范围;当
的取值范围;当![]() 为何值时,
为何值时,![]() 有最大值或最小值.
有最大值或最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,DE垂直平分AB,分别交AB,AC于点E,D.

(1)若∠ADE=40°,求∠DBC的度数;
(2)若BC=6,△CDB的周长为15,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )

A. ﹣2 B. ﹣3 C. ﹣![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.

(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人用微信聊天、转账、付款等.把微信账户里的钱转到银行卡叫做提现.自2016年3月1日起,每个微信账户有1000元的免费提现额度,当累计提现超过这个额度时,超出的部分需要付0.1%的手续费.
(1)小明的妈妈从未提现过,此时想把微信零钱里的15000元提现,那么将收取手续费 元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第一次提现 | 第二次提现 | 第三次提现 | |
提现金额(元) | a | b | 3a+2b |
手续费(元) | 0 | 0.4 | 3.4 |
①二元一次方程组的相关知识求表中a、b的值;
②小明3次提现金额共计 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面图形上的任意两点![]() ,
,![]() ,如果经过某种变换(如:平移、旋转、轴对称等)得到新图形上的对应点
,如果经过某种变换(如:平移、旋转、轴对称等)得到新图形上的对应点![]() ,
,![]() ,保持
,保持![]() ,我们把这种对应点连线相等的变换称为“同步变换”.对于三种变换:
,我们把这种对应点连线相等的变换称为“同步变换”.对于三种变换:
①平移、②旋转、③轴对称,
其中一定是“同步变换”的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.
(1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m,n件产品(甲厂的日均产量与2018年相同),m:n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com