
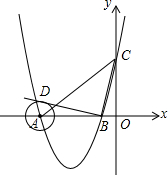
 如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).分析 (1)设抛物线的解析式为y=a(x+3)2-4,将(0,5)代入可求得a的值,从而得到抛物线的解析式;
(2)先求得A、B的坐标,从而可求得AB、BC的长,过点A作AE⊥BD,垂足为E.然后△ABE∽△BCD,由相似三角形的性质可求得AE的长;
(3)先求得直线AC的解析式,由相互垂直的直线的特点可知AP的一次项系数为-1,分别∠PAC=90°,∠ACP=90°两种情况求得AP的解析式,然后在求得AP与抛物线的交点P的坐标即可.
解答 解:(1)设抛物线的解析式为y=a(x+3)2-4,
∵把(0,5)代入得5=9a-4,解得a=1,
∴抛物线的解析式为y=(x+3)2-4,即y=x2+6x+5.
(2)如图1所示,过点A作AE⊥BD,垂足为E.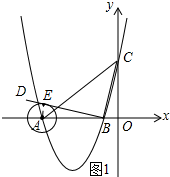
令y=0,得(x+3)2-4=0,解得:x1=-5,x2=-1,则A(-5,0)、B(-1,0).
在Rt△COB中,由勾股定理可知:BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{26}$.
∵A(-5,0)、B(-1,0),
∴AB=4.
∵∠CBE=90°,
∴∠CBO+∠EBA=90°.
又∵∠EBA+∠EAB=90°,
∴∠EAB=∠CBO.
又∵∠AEB=∠COB,
∴△ABE∽△BCD.
∴$\frac{AE}{AB}=\frac{OB}{CB}$,即$\frac{AE}{4}=\frac{1}{\sqrt{26}}$.
解得:AE=$\frac{2\sqrt{26}}{13}$.
∴⊙A的半径为$\frac{2\sqrt{26}}{13}$.
(3)设AC的解析式为y=kx+b.
∵将(-5,0)、(0,5)代入得:$\left\{\begin{array}{l}{b=5}\\{-5k+b=0}\end{array}\right.$,解得:b=5,k=1,
∴直线AC的解析式为y=x+5.
如图2所示:当∠CAP=90°时.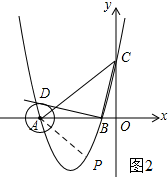
∵AP⊥AC,
∴直线AP的一次项系数为-1.
设直线AP的解析式为y=-x+b1,将(-5,0)代入得:5+b1=0,解得:b1=-5,则直线AP的解析式为y=-x-5.
将y=-x-5与y=x2+6x+5联立得:$\left\{\begin{array}{l}{y=-x-5}\\{y={x}^{2}+6x+5}\end{array}\right.$,解得:x1=-2,x2=-5(舍去).
∵将x=-2代入y=-x-5得:y=-3,
∴点P的坐标为(-2,-3).
如图3所示:当∠ACP=90°时.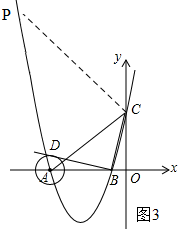
设直线AP的解析式为y=-x+b2,将(0,5)代入得:b2=5,则直线AP的解析式为y=-x+5.
将y=-x+5与y=x2+6x+5联立得:$\left\{\begin{array}{l}{y=-x+5}\\{y={x}^{2}+6x+5}\end{array}\right.$,解得:x1=-7,x2=0(舍去).
∵将x=-7代入y=-x+5得:y=12,
∴点P的坐标为(-7,12).
综上所述,点P的坐标为(-2,-3)或(-7,12).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、相似三角形的性质和判定、相互垂直的两直线的特点,掌握抛物线的顶点式是解决问题(1)的关键,证得△ABE∽△BCD是解决问题(2)的关键,求得直线AP的解析式是解决问题(3)的关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).
如图,在平面直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第五个等腰直角三角形的斜边AG长为( )
如图,已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第五个等腰直角三角形的斜边AG长为( )| A. | 4$\sqrt{2}$ | B. | 5$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在美化城市的建设中,某街道想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.
在美化城市的建设中,某街道想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com