
【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)求二月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型每台进价为3500元,乙型每台进价为4000元,预计用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)对于(2)中刚进货的20台两种型号的手机,该店计划对甲型号手机在二月份售价基础上每售出一台甲型手机再返还顾客现金a元,乙型手机按销售价4400元销售,若要使(2)中所有方案获利相同,a应取何值?
【答案】(1)二月份甲型号手机每台售价为4000元;(2)有三种购货方案:一、甲型手机8台,乙型手机12台;二、甲型手机9台,乙型手机11台;三、甲型手机10台,乙型手机10台;(3)a=100
【解析】试题分析:(1)设二月份甲型号手机每台售价为x元,则一月份甲型手机的每台售价为(x+500)元,根据题意建立方程就可以求出其值;
(2)设购甲型手机y台,则购乙型手机(20-y)台,根据题意建立不等式组,求出其解就可以得出结论;
(3)求出每台的利润根据不同的购买方案求出表示出相应的利润,再由条件三种方案的利润相等就可以建立方程求出其值.
试题解析:
(1)设二月份甲型号手机每台售价为x元,则一月份甲型手机的每台售价为(x+500)元,根据题意,得
![]()
解得:x=4000,
经检验,x=4000是原方程的根,
故原方程的根是x=4000.
故二月份甲型号手机每台售价为4000元;
(2)设购甲型手机y台,则购乙型手机(20y)台,由题意得:
750003500y+4000(20y)76000,
解得![]()
∵y为整数,
∴y=8,9,10,
∴乙型手机的台数为:12,11,10.
∴有三种购货方案:一、甲型手机8台,乙型手机12台;
二、甲型手机9台,乙型手机11台;
三、甲型手机10台,乙型手机10台;
(3)根据题意,得
500×88a+400×12=500×99a+400×11,
解得:a=100.


科目:初中数学 来源: 题型:
【题目】请你画出一个以BC为底边的等腰ΔABC,使底边上的高AD=BC.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
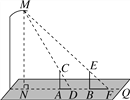
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣![]() x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
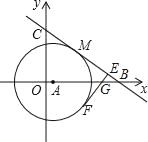
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 是
是![]() 边上的点(不与
边上的点(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,下列表述错误的是( )
,下列表述错误的是( )
A. 若![]() 是
是![]() 边的中线,则
边的中线,则![]()
B. 若![]() 是
是![]() 边的高线,则
边的高线,则![]()
C. 若![]() 是
是![]() 的平分线,则
的平分线,则![]() 与
与![]() 的面积相等
的面积相等
D. 若![]() 是
是![]() 的平分线又是
的平分线又是![]() 边的中线,则
边的中线,则![]() 为
为![]() 边的高线
边的高线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
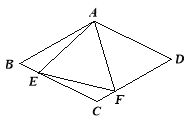
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com