
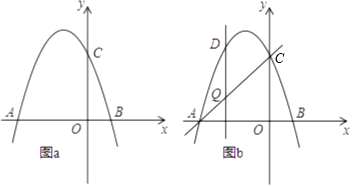
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值
【答案】
(1)
解:把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
![]() ,
,
解得 ![]() .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)
解:由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴ ![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±2 ![]() .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2 ![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2 ![]() ,﹣4)
,﹣4)
(3)
解:设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得 ![]() ,
,
解得 ![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+ ![]() )2+
)2+ ![]() ,
,
∴当x=﹣ ![]() 时,QD有最大值
时,QD有最大值 ![]()
【解析】(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;(2)设P点坐标为(x,﹣x2﹣2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;(3)先运用待定系数法求出直线AC的解析式为y=x+3,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)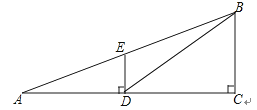
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧 ![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证: 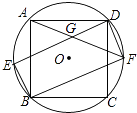
(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=﹣1,下列结论:
①abc<0;②2a+b=0;③a﹣b+c>0;④4a﹣2b+c<0
其中正确的是( )
A.①②
B.只有①
C.③④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境: 
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境: 
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正七边形ABCDEFG,请仅用无刻度的直尺,分别按下列要求画图. 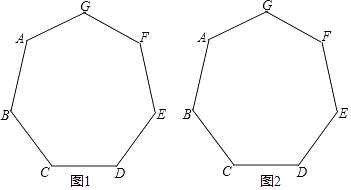
(1)在图1中,画出一个以AB为边的平行四边形;
(2)在图2中,画出一个以AF为边的菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com