练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若抛物线y=ax2+bx+c（a≠0）的图象与抛物线y=x2﹣4x+3的图象关于y轴对称，则函数y=ax2+bx+c的解析式为__________．


    y=x2+4x+3．

    【考点】二次函数图象与几何变换．

    【专题】常规题型．

    【分析】本可直接利用关于y轴对称的点的坐标特点，横坐标变为相反数，纵坐标不变解答．

    【解答】解：∵抛物线y=ax2+bx+c（a≠0）的图象与抛物线y=x2﹣4x+3的图象关于y轴对称，

    ∴函数y=ax2+bx+c的解析式为：y=（﹣x）2﹣4（﹣x）+3=x2+4x+3．

    故答案为：y=x2+4x+3．

    【点评】本题考查了二次函数图象与几何变换，明确关于y轴对称的函数顶点纵坐标相同，横坐标互为相反数，难度一般．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


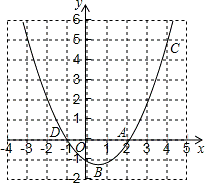
    如图，已知二次函数y=ax2+bx+c的图象过A（2，0），B（0，﹣1）和

    C（4，5）三点．

    （1）求二次函数的解析式；

    （2）设二次函数的图象与x轴的另一个交点为D，求点D的坐标；

    （3）在同一坐标系中画出直线y=x+1，并写出当x在什么范围内时，
    一次函数的值大于二次函数的值．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知△ABC中，∠C=90°，∠B=2∠A,  BC=3cm,则AB=      _cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若（2，5）、（4，5）是抛物线y=ax2+bx+c上的两个点，则它的对称轴是(     )

    A．x=﹣      B．x=1   C．x=2   D．x=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列命题：

    ①若a+b+c=0，则b2﹣4ac＜0；

    ②若b=2a+3c，则一元二次方程ax2+bx+c=0有两个不相等的实数根；

    ③若b2﹣4ac＞0，则二次函数y=ax2+bx+c的图象与坐标轴的交点的个数是2或3；

    ④若b＞a+c，则一元二次方程ax2+bx+c=0有两个不相等的实数根．

    其中正确的是(     )

    A．②④ B．①③  C．②③ D．③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．阅读下面的例题，解方程（x﹣1）2﹣5|x﹣1|﹣6=0，解方程x2﹣|x|﹣2=0；

    解：原方程化为|x|2﹣|x|﹣2=0．令y=|x|，原方程化成y2﹣y﹣2=0

    解得：y1=2y2=﹣1

    当|x|=2，x=±2；当|x|=﹣1时（不合题意，舍去）

    ∴原方程的解是x1=2，x2=﹣2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    从正方形的铁片上，截去2cm宽的一条长方形，余下的面积是48cm2，则原来的正方形铁片的面积是(     )

    A．96cm2      B．64cm2      C．54cm2      D．52cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    3m2﹣7m﹣4=0；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    单项式的系数和次数分别是（   ）

    A．，5     B．，6      C．，7      D． ，6

    查看答案和解析>>

    同步练习册答案