
分析 (1)根据平均数的计算公式和方差分别进行计算即可得出答案;
(2)先抽取样本容量为20的两个样本,再根据平均数和方差公式进行计算,最后比较即可得出答案.
解答 解:(1)这50名学生身高的平均数是:(150+148+159+156+157+163+…+162)÷50=160.58(cm),
方差是:$\frac{1}{50}$=[(147-160.58)2+(148-160.58)2+(150-160.58)2+(151-160.58)2+(152-160.58)2+2(153-160.58)2+…+(162-160.58)2]≈44.56;
(2)根据题意得:样本(1)是:150,148,159,156,157,163,156,164,156,159,169,163,170,162,163,164,155,162,153,155;
样本(2)是:162,165,159,147,163,172,156,165,157,164,152,156,153,164,165,162,167,151,175,162.
样本(1)的平均数是:(150+148+159+156+157…+155)÷20=159.2(cm),
样本(2)的平均数是:(162+165+159+147+…+162)÷20=160.85(cm),
样本(1)的方差是:$\frac{1}{20}$=[(148-159.2)2+(150-159.2)2+(153-159.2)2+2(155-159.2)2+…+(170-159.2)2]≈27.09;
样本(2)的方差是:$\frac{1}{20}$=[(147-160.85)2+(151-160.85)2+(152-160.85)2+(153-160.85)2+2(156-160.85)2+…+(175-160.85)2]≈46.78;
它们的结果一致,与总体的结果一致.
点评 此题考查了平均数和方差,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
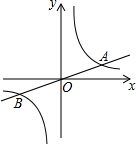 如图所示:已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A,B两点,且点A的横坐标为4
如图所示:已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A,B两点,且点A的横坐标为4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
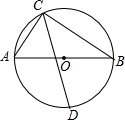 如图,AB为⊙O的直径,点C在⊙O上,连接AC和BC,∠ACB的平分线交⊙O于点D,
如图,AB为⊙O的直径,点C在⊙O上,连接AC和BC,∠ACB的平分线交⊙O于点D,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
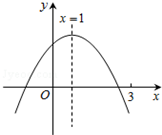 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有②③⑤.
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com