
 在正方形ABCD中,AB=4,动点E在AB上(0<EA<2),现将正方形沿着过E点的直线翻折,使得点B落在边AD上的点F,翻折后边BC所在的直线与DC交于G.
在正方形ABCD中,AB=4,动点E在AB上(0<EA<2),现将正方形沿着过E点的直线翻折,使得点B落在边AD上的点F,翻折后边BC所在的直线与DC交于G.| FD |
| AE |
| C△DFG |
| C△AEF |
| 64-y2 |
| 8-x |
| FD |
| AE |
| C△DFG |
| C△AEF |
| 8-y |
| 8-x |
| C△DFG |
| 8+y |
| 64-y2 |
| 8-x |


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
 数学小组的同学为了解2014年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将数据进行了整理:
数学小组的同学为了解2014年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将数据进行了整理:| 月均用水量x(t) | 频数 | 频率 |
| 0<x≤5 | 12 | 0.15 |
| 5<x≤10 | a | 0.35 |
| 10<x≤15 | 12 | 0.15 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 8 | b |
| 25<x≤30 | 4 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:
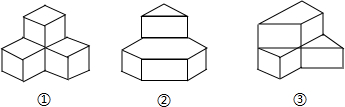
| A、②③④ | B、①②③ |
| C、①②④ | D、①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,折线ABC是一个路灯的示意图,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,在地面上距离A点8米的点E处,测得点B的仰角是45°,点C的仰角是60°,点E、D、A在一条直线上.求点C到地面的距离CD.(
如图,折线ABC是一个路灯的示意图,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,在地面上距离A点8米的点E处,测得点B的仰角是45°,点C的仰角是60°,点E、D、A在一条直线上.求点C到地面的距离CD.(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.
数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com