
 数学小组的同学为了解2014年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将数据进行了整理:
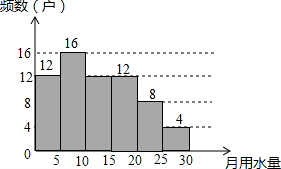
数学小组的同学为了解2014年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将数据进行了整理:| 月均用水量x(t) | 频数 | 频率 |
| 0<x≤5 | 12 | 0.15 |
| 5<x≤10 | a | 0.35 |
| 10<x≤15 | 12 | 0.15 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 8 | b |
| 25<x≤30 | 4 | 0.05 |
 ;
;| 12+16+12+12 |
| 80 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 △ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,连接DA并延长至点E,使∠ACB=∠ECD.
△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,连接DA并延长至点E,使∠ACB=∠ECD.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,AB=AC(∠BAC<60°),将腰AB绕点A逆时针旋转60°,得线段AD,连接BD、CD,将底BC绕点B逆时针旋转60°,得线段BE,连接AE.
如图,△ABC中,AB=AC(∠BAC<60°),将腰AB绕点A逆时针旋转60°,得线段AD,连接BD、CD,将底BC绕点B逆时针旋转60°,得线段BE,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:
 在正方形ABCD中,AB=4,动点E在AB上(0<EA<2),现将正方形沿着过E点的直线翻折,使得点B落在边AD上的点F,翻折后边BC所在的直线与DC交于G.
在正方形ABCD中,AB=4,动点E在AB上(0<EA<2),现将正方形沿着过E点的直线翻折,使得点B落在边AD上的点F,翻折后边BC所在的直线与DC交于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com