【题目】如图，过点B，D分别向线段AE作垂线段BQ和DF，点Q和F是垂足，连结AB，DE，BD，BD交AE于点C，且AB＝DE，AF＝EQ．
(1)求证：△ABQ≌△EDF；
(2)求证：C是BD的中点．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2.
证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a，
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab．
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a（b﹣a）
∴ 12 b2+ 12 ab= 12 c2+ 12 a（b﹣a）
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明．
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，函数y＝﹣3x+b的图象与y轴相交于点B，与函数y＝﹣
x的图象相交于点A，且OB＝5．
（1）求点A的坐标；
（2）求函数y＝﹣3x+b、y＝﹣x的图象与x轴所围成的三角形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2﹣4ax+3a．
（Ⅰ）求该二次函数的对称轴；
（Ⅱ）若该二次函数的图象开口向下，当1≤x≤4时，y的最大值是2，且当1≤x≤4时，函数图象的最高点为点P，最低点为点Q，求△OPQ的面积；
（Ⅲ）若对于该抛物线上的两点P（x1，y1），Q（x2，y2），当t≤x1≤t+1，x2≥5时，均满足y1≥y2，请结合图象，直接写出t的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等边△ABC的边长为8，点P是AB边上的一个动点（与点A、B不重合），直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.
（1）如图1，当PB=4时，若点B’恰好在AC边上，则AB’的长度为_____；
（2）如图2，当PB=5时，若直线l//AC，则BB’的长度为 ；
（3）如图3，点P在AB边上运动过程中，若直线l始终垂直于AC，△ACB’的面积是否变化？若变化，说明理由；若不变化，求出面积；
（4）当PB=6时，在直线l变化过程中，求△ACB’面积的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，下述结论：(1)BD平分∠ABC；(2)AD=BD=BC；(3)△BDC的周长等于AB+BC；(4)D是AC中点．其中正确的命题序号是（ ）
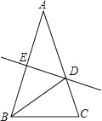
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系，根据图象解决以下问题：
（1）慢车的速度为_____km/h，快车的速度为_____km/h；
（2）解释图中点C的实际意义并求出点C的坐标；
（3）求当x为多少时，两车之间的距离为500km．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
