
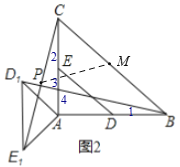
【题目】在![]() 中,
中,![]() 分别是
分别是![]() 的中点,若等腰
的中点,若等腰![]() 绕点
绕点![]() 逆时针旋转,得到等腰
逆时针旋转,得到等腰![]() ,设旋转角为
,设旋转角为![]() ,记直线
,记直线![]() 与
与![]() 的交点为
的交点为![]()


(1)如图![]() ,当
,当![]() 时,线段
时,线段![]() 的长等于 ,线段
的长等于 ,线段![]() 的长等于 .(直接填写结果)
的长等于 .(直接填写结果)
(2)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ,且
,且![]() ;
;
(3)设![]() 的中点为
的中点为![]() ,则线段
,则线段![]() 的长为 (直接填写结果).
的长为 (直接填写结果).
【答案】(1)![]() ;
; ![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)利用等腰直角三角形的性质结合勾股定理即可求得答案;
(2)根据旋转的性质得出![]() ,继而证明
,继而证明![]() ,即可推得答案;
,即可推得答案;
(3)利用直角三角形斜边中线的性质即可求得答案.
(1)∵∠BAC=90°,AC=AB=4,D、E分别是边AB、AC的最短,
∴AE=AD=2,
∵等腰![]() 绕点
绕点![]() 逆时针旋转,得到等腰
逆时针旋转,得到等腰![]() ,设旋转角为
,设旋转角为![]() ,
,
∴当α=90°时,AE1=2,∠E1AE=90°,
∴BD1=![]() ,CE1=
,CE1=![]() ,
,
故答案为:![]() ;
; ![]() ;
;
(2)当![]() 时,
时,
![]() 是由
是由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到,
得到,
![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
![]() ,
,
![]() ,
,
记直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,
![]() ;
;
(3)如图2,由(2)的证明可知旋转角为α时,易证得![]() ,
,
∴∠1=∠2,
又∵∠3=∠4,∠1+∠4+∠BAC=180°,∠2+∠3+∠BPC=180°,
∴∠CPB=∠CAB=90°,
又∵M为BC的中点,
∴PM=![]() BC,
BC,
∴PM=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】你知道古代数学家怎样解一元二次方程吗?以x2﹣2x﹣3=0为例,大致过程如下:第一步:将原方程变形为x2﹣2x=3,即x(x﹣2)=3.
第二步:构造一个长为x,宽为(x﹣2)的长方形,长比宽大2,且面积为3,如图所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图所示.
第四步:计算大正方形面积用x表示为 .长方形面积为常数 .小正方形面积为常数 .
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程 ,两边开方可求得:x1=3,x2=﹣1.
(1)第四步中横线上应填入 ; ; ; .
(2)请参考古人的思考过程,画出示意图,写出步骤,解方程x2﹣x﹣1=0.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为每千克30元的水产品,据市场分析,若按每千克40元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种情况,请解答以下问题:
(1)当销售单价定为每千克45元时,计算月销售量和月销售利润;
(2)该商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车从A地驶往B地,前![]() 路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用一元一次方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() =2
=2![]() ,
,![]() 为
为![]() 的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
的中点,请仅用无刻度的直尺分别按下列要求画图(保留作图痕迹)
(1)在图1中,画出△ABD的BD边上的中线;
(2)在图2中,若BA=BD, 画出△ABD的AD边上的高 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,矩形
,矩形![]() 的两条边
的两条边![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
轴上,已知点![]() 、点
、点![]() .
.
(1)若把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,求折痕
,求折痕![]() 的长;
的长;
(2)在(1)的条件下,点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图![]() ,若
,若![]() 为
为![]() 边上的一动点,在
边上的一动点,在![]() 上取一点
上取一点![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 顺时针旋转一周,在旋转的过程中,
顺时针旋转一周,在旋转的过程中,![]() 的对应点为
的对应点为![]() ,请直接写出
,请直接写出![]() 的最大值和最小值.
的最大值和最小值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民月用水量,某市对某区居民用水量进行了抽样调查,并制成如下直方图.

(1)这次一共抽查了____户;
(2)用水量不足10吨的有____户,用水量超过16吨的有____户;
(3)假设该区有8万户居民,估计用水量少于10吨的有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
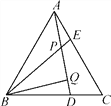
【题目】如图,等边△ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q.
(1)求证:BP=2PQ;
(2)若PE=1,PQ=3,试求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com