
如图直线y=kx+6与x轴y轴分别交于点E、F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为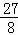 ,并说明理由.
,并说明理由.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
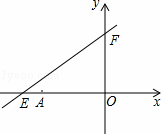
如图所示,在平行四边形ABCD纸片中,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C且点B、A、B'处于同一直线上,
(1)求证:以A、C、D、B′为顶点的四边形是矩形.
(2)若四边形ABCD的面积为12cm2,求翻折后纸片重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
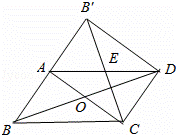
如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
温度与我们的生活息息相关,你仔细观察过温度计吗?如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉),设摄氏温度为x(℃),华氏温度为y(℉),则y是x的一次函数.
(1)仔细观察图中数据,试求出y与x之间的函数表达式;
(2)当摄氏温度为零下15℃时,求华氏温度为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
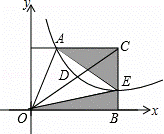
如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=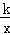 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
(1)填空:双曲线的另一支在第三象限,k的取值范围是k>0;
(2)若点C的坐标为(1,1),请用含有k的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
(3)若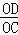 =
=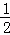 ,S△OAC=2,求双曲线的解析式.
,S△OAC=2,求双曲线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
对于实数a、b,定义运算“*”:a*b=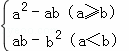 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com