
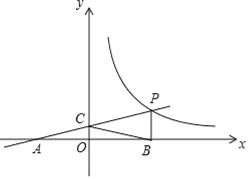
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
【答案】(1)反比例函数解析式为y=![]() ,一次函数解析式为y=
,一次函数解析式为y=![]() x+1;
x+1;
(2)证明见解析;
(3)满足条件的点D,其坐标为(8,1).
【解析】试题分析:(1)由条件可求得P点坐标,利用待定系数法可求得一次函数和反比例函数的解析式;
(2)由平行线分线段成比例可求得AC=PC,可证得结论;
(3)可先求得C点坐标,过C作CD∥x轴,交PB于点E,交反比例函数图象于点D,可求得此时D点坐标,可证得四边形BCPD为菱形.
试题解析:(1)∵点A与点B关于y轴对称,
∴AO=BO,
∵A(﹣4,0),
∴B(4,0),
∵PB⊥x轴于点B,
∴P(4,2),
把P(4,2)代入反比例函数解析式可得m=8,
∴反比例函数解析式为y=![]() ,
,
把A、P两点坐标代入一次函数解析式可得![]() ,解得
,解得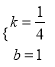 ,
,
∴一次函数解析式为y=![]() x+1;
x+1;
(2)证:∵点A与点B关于y轴对称,
∴OA=OB,
∵PB⊥x轴于点B,
∴∠PBA=∠COA=90°,
∴PB∥CO,
∴![]() =1,即AC=PC,
=1,即AC=PC,
∴点C为线段AP的中点;
(3)存在点D,使四边形BCPD为菱形.
理由如下:
∵点C为线段AP的中点,
∴BC=![]() AP=PC,
AP=PC,
∴BC和PC是菱形的两条边,
由y=![]() x+1可得C(0,1),
x+1可得C(0,1),
如图,过点C作CD∥x轴,交PB于点E,交反比例函数图象于点D,分别连接PD、BD,

∴D(8,1),且PB⊥CD,
∴PE=BE=1,CE=DE=4,
∴PB与CD互相垂直平分,即四边形BCPD为菱形,
∴存在满足条件的点D,其坐标为(8,1).


科目:初中数学 来源: 题型:
【题目】某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九(三)班的演唱打分情况为:89,92,92,95,95,96,97,从中去掉一个最高分和一个最低分,余下的分数的平均数是最后得分,则该班的得分为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解八年级500名学生的身体素质情况,体育老师对八年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图如下所示:

请结合图表完成下列问题:
(1)表中的m= , 次数在140≤x<160这组的频率为;
(2)请你把频数分布直方图补充完整;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,求八年级合格的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个球,其中7个黄球,8个黑球,5个红球,这些球只有颜色不同,其它都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数 ![]() 的图像与x轴、y轴分别交于点A、B,与函数
的图像与x轴、y轴分别交于点A、B,与函数 ![]() 的图像交于点M,点M的横坐标为2.
的图像交于点M,点M的横坐标为2.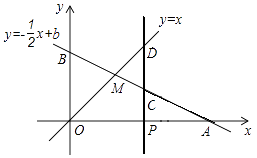
(1)求点A的坐标;
(2)在x轴上有一点动点P ![]() (其中
(其中 ![]() >2),过点P作x轴的垂线,分别交函数
>2),过点P作x轴的垂线,分别交函数 ![]() 和
和 ![]() 的图像于点C、D,且OB=2CD,求
的图像于点C、D,且OB=2CD,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
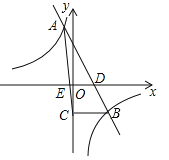
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com