
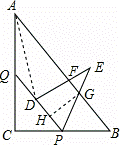
如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
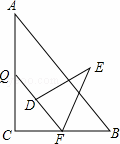
(1)证明:∵在Rt△ABC中,AB=15,BC=9,
∴AC= =
= =12.
=12.
∵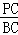 =
=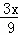 =
=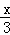 ,
,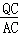 =
=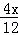 =
=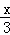 ,
,
∴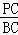 =
=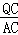 .
.
∵∠C=∠C,
∴△PQC∽△BAC,
∴∠CPQ=∠B,
∴PQ∥AB;
(2)解:连接AD,
∵PQ∥AB,
∴∠ADQ=∠DAB.
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ.
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
∴DQ=2x.
∵AQ=12﹣4x,
∴12﹣4x=2x,解得x=2,
∴CP=3x=6.
(3)解:当点E在AB上时,
∵PQ∥AB,
∴∠DPE=∠PEB.
∵∠CPQ=∠DPE,∠CPQ=∠B,
∴∠B=∠PEB,
∴PB=PE=5x,
∴3x+5x=9,解得x=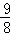 .
.
①当0<x≤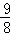 时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤
时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤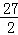 ;
;
②当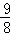 <x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,
<x<3时,设PE交AB于点G,DE交AB于F,作GH⊥FQ,垂足为H,
∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,
∴ =
=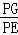 =
=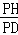 .
.
∵PG=PB=9﹣3x,
∴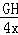 =
=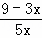 =
=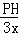 ,
,
∴GH=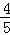 (9﹣3x),PH=
(9﹣3x),PH=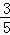 (9﹣3x),
(9﹣3x),
∴FG=DH=3x﹣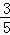 (9﹣3x),
(9﹣3x),
∴T=PG+PD+DF+FG=(9﹣3x)+3x+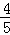 (9﹣3x)+[3x﹣
(9﹣3x)+[3x﹣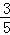 (9﹣3x)]
(9﹣3x)]
=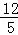 x+
x+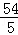 ,
,
此时,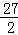 <T<18.
<T<18.
∴当0<x<3时,T随x的增大而增大,
∴T=12时,即12x=12,解得x=1;
TA=16时,即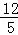 x+
x+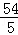 =16,解得x=
=16,解得x=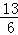 .
.
∵12≤T≤16,
∴x的取值范围是1≤x≤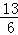 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
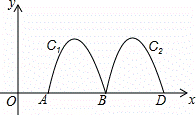
如图,抛物线y=﹣2x 2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A. ﹣2<m<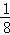 B. ﹣3<m<﹣
B. ﹣3<m<﹣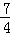 C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣ 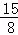
查看答案和解析>>
科目:初中数学 来源: 题型:
由大小两种货车,3辆大车与4辆小车一次可以运货22吨,2辆大车与6辆小车一次可以运货23吨.请根据以上信息,提出一个能用方程(组)解决的问题,并写出这个问题的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )
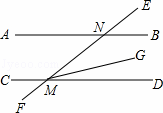
A.15° B. 30° C. 75° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
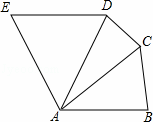
A.150° B. 160° C. 130° D. 60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com