
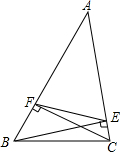
 如图,在△ABC中,BE、CF分别是AC、AB边上的高,∠A=45°,求S△AEF:S四边形FBCE.
如图,在△ABC中,BE、CF分别是AC、AB边上的高,∠A=45°,求S△AEF:S四边形FBCE. 分析 通过已知条件证得△ABE∽△ACF,得到$\frac{AF}{AE}=\frac{AC}{AB}$,即$\frac{AF}{AC}=\frac{AE}{AB}$,且∠FAE=∠CAB,推出△ABC∽△AEF,证得△AFC是等腰直角三角形,得到$\frac{AF}{AC}=\frac{AE}{AB}$=$\frac{\sqrt{2}}{2}$,求出$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AF}{AC}$)2=$\frac{1}{2}$,于是得到结果.
解答 解:∵BE、CF是高,
∴∠AEB=∠AFC=90°,且∠BAE=∠CAF,
∴△ABE∽△ACF,
∴$\frac{AF}{AE}=\frac{AC}{AB}$,
即$\frac{AF}{AC}=\frac{AE}{AB}$,且∠FAE=∠CAB,
∴△ABC∽△AEF,
∵∠A=45°,
∴△AFC是等腰直角三角形,
∴AC=$\sqrt{2}$AF,
∴$\frac{AF}{AC}=\frac{AE}{AB}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{AF}{AC}$)2=$\frac{1}{2}$,
∴S△AEF:S四边形FBCE=1:1.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形对应边成比例、面积比等于相似比的平方是解题的关键.


科目:初中数学 来源: 题型:解答题
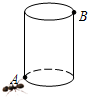 如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).
如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3≤y≤1 | B. | -7≤y≤1 | C. | -7≤y≤11 | D. | -7≤y<11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
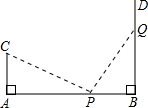 如图,AB=12米,CA⊥AB,垂足为点A,DB⊥AB,垂足为B,动点P从点B沿BA向点A方向移动,每分钟走1m,同时,点Q从点B沿BD向点D方向移动,每分钟走2m,已知CA=4m,几分钟后,△CAP≌PBQ?说明理由.
如图,AB=12米,CA⊥AB,垂足为点A,DB⊥AB,垂足为B,动点P从点B沿BA向点A方向移动,每分钟走1m,同时,点Q从点B沿BD向点D方向移动,每分钟走2m,已知CA=4m,几分钟后,△CAP≌PBQ?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-1=(2x+1)(2x-1) | B. | x+2y=(x+y)+y | C. | 3x2+6x=3x(x+2) | D. | x2-2x+3=x(x-2)+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com