
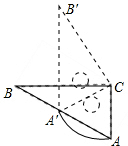
 如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)
如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π) 科目:初中数学 来源: 题型:选择题
| A. | 50名学生 | B. | 50名学生的身高 | C. | 400名学生 | D. | 400名学生的身高 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
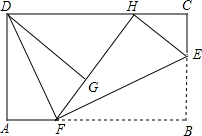 如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B
如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B查看答案和解析>>
科目:初中数学 来源: 题型:选择题
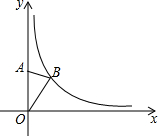 如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )| A. | 逐渐减小 | B. | 逐渐增大 | C. | 先增大后减小 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
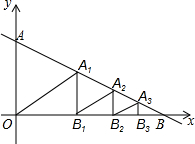 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{4}^{n-1}}$ | D. | $\frac{1}{{4}^{n}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
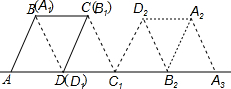 如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.
如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com