
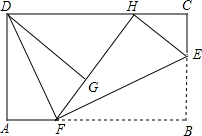
 如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B
如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B分析 (1)根据余角的定义,可得∠CEH的度数,根据角的和差,可得∠HEB的度数,根据翻折的性质,可得∠EHF的度数,根据四边形内角和,可得∠HFB的度数,根据邻补角的定义,可得答案;
(2)根据翻折的性质,可得∠BFE=∠HFE,∠AFD=∠GFD,根据角的和差,等式的性质,可得答案.
解答 解:(1)由余角的定义,得
∠CEH=90°-∠CHE=50°
由角的和差,得
∠HEB=180°-∠CEH=180°-50°=130°,
由翻折的性质,得
∠B=∠EHF=90°,
由四边形内角和,得
∠HFB=360°-∠B-∠BEH-∠EHF=50°,
由邻补角的定义,得
∠HFA=180°°-∠HFB=130°;
(2)DF和线段EF位置关系是DF⊥EF,
证明:∵长方形ABCD沿EF折叠后点B恰好落在CD边上的点H处,将△DAF沿DF折叠后点A恰好落在HF上的点G处,
∴∠BFE=∠HFE,∠AFD=∠GFD.
∵∠BFE+∠HFE+∠AFD+∠GFD=180°,
∴∠DFG+∠GFE=90°,
即∠DFE=90°,
∴DF⊥EF.
点评 本题考查了翻折变换,利用了余角的定义,角的和差,翻折的性质,四边形内角和,邻补角的定义,利用知识点较多,题目稍微有点难度.


科目:初中数学 来源: 题型:选择题
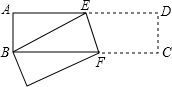 已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与D重合,折痕为EF,则BE的长为( )
已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与D重合,折痕为EF,则BE的长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
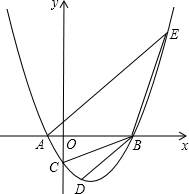 设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1,0)、B(4,0),与y轴交于点C.
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1,0)、B(4,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
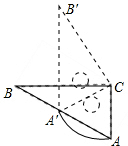 如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)
如图,Rt△ABC中,∠B=30°,斜边AB长12为cm,绕直角顶点C顺时针旋转,当点A落在AB边上的A′处,则弧AA′的长为2π cm.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两条直线被第三条直线所截,则同旁内角互补 | |
| B. | 点到直线的距离是指直线外一点到这条直线的垂线段 | |
| C. | $\sqrt{81}$的算术平方根是9 | |
| D. | 同一平面内,若直线a∥b,a⊥c,则b⊥c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 属于随机事件 | B. | 可能性大小为$\frac{1}{4}$ | C. | 属于不可能事件 | D. | 是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com