
分析 (1)先把三个方程相加可得到x+y+z=7,然后利用加减消元法分别求出x、y、z即可;
(2)利用a:b:c=4:5:6,设a=3x,b=4x,c=5x,代入第二方程得到3x+4x+5x=36,解得x=3,然后分别计算a、b、c;
(3)先把方程组整理为$\left\{\begin{array}{l}{3x+2y-6z=-30①}\\{2x-3y+z=60②}\\{6x-4y-3z=72③}\end{array}\right.$,接着利用加减消元法消去z得到关于x、y的方程组,可求出x、y,然后利用代入法求出z即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+3y+2z=19①}\\{3x+2y+2z=17②}\\{2x+2y+3z=13③}\end{array}\right.$,
①+②+③得7x+7y+7z=49,
所以x+y+z=7④,
②-④×2得x=3,
①-④×2得y=5,
③-④×2得z=-1,
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=5}\\{z=-1}\end{array}\right.$;
(2)设a=3x,则b=4x,c=5x,
所以3x+4x+5x=36,解得x=3,
所以a=9,b=12,c=15;
即方程组的解为$\left\{\begin{array}{l}{a=9}\\{b=12}\\{c=15}\end{array}\right.$;
(3)方程组整理为$\left\{\begin{array}{l}{3x+2y-6z=-30①}\\{2x-3y+z=60②}\\{6x-4y-3z=72③}\end{array}\right.$,
②×6+①得15x-16y=330④,
②×3+③得12x-13y=252⑤,
解④⑤组成的方程组得x=86,y=60,
把x=86,y=60代入②得172-180+z=60,解得z=68,
所以方程组的解为$\left\{\begin{array}{l}{x=86}\\{y=60}\\{z=68}\end{array}\right.$.
点评 本题考查了解三元一次方程组:利用加减消元法或代入消元法把解三元一次方程组的问题转化为解二元一次方程组.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
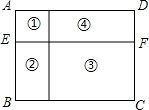 如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.
如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
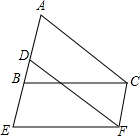 如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.
如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com