Question

17．某班在元旦游戏活动中，有一个摸奖游戏，规则如下：不透明的盒子内有4个除颜色外完全相同的球，其中有2个红球，2个白球，摇匀后让同学们去盒子内摸球，摸到红球的就获奖，摸到白球的不获奖．
（1）现小颖有一次摸球机会，她从盒子中随机摸出1个球，求小颖获奖的概率；
（2）如果小颖、小明都有两次摸球的机会，小颖先摸出1个球，放回后再摸出1个球；小明同时摸出2个球；他们摸出的2个球中只要有红球就获奖，他们获奖的机会相等吗？请用树状图（或列表）的方法说明理由．

Answer 1

分析 （1）直接利用概率公式求解；
（2）对于小颖先摸出1个球，放回后再摸出1个球可画树状图展示所有16种等可能的结果数，找出两个球中有红球的结果数，利用概率公式可计算出小颖获奖的概率=$\frac{3}{4}$；对于小明同时摸出2个球，画树状图展示所有12种等可能的结果数，再找出两个球中有红球的结果数为，利用概率公式计算出小颖获奖的概率，然后比较两概率的大小即可判断他们获奖的机会是否相等．

解答 解：（1）小颖获奖的概率=$\frac{2}{2+2}$=$\frac{1}{2}$；
（2）小颖先摸出1个球，放回后再摸出1个球，
画树状图为：

共有16种等可能的结果数，其中两个球中有红球的结果数为12，
所以小颖获奖的概率=$\frac{12}{16}$=$\frac{3}{4}$；
小明同时摸出2个球，
画树状图为：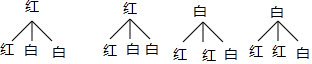

共有12种等可能的结果数，其中两个球中有红球的结果数为10，
所以小颖获奖的概率=$\frac{10}{12}$=$\frac{5}{6}$，
而$\frac{3}{4}$≠$\frac{5}{6}$，
所以他们获奖的机会不相等．

点评 本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．