Question

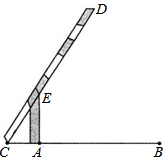
如图，小明在研究性学习活动中，对自己家所在的小区进行调查后发现，小区汽车入口宽AB为3.2m，在入口的一侧安装了停止杆CD，其中AE为支架．当停止杆仰起并与地面成60°角时，停止杆的端点C恰好与地面接触．此时CA为0.7m．在此状态下，若一辆货车高3m，宽2.5m，入口两侧不能通车，那么这辆货车在不碰杆的情况下，能从入口内通过吗？请你通过估算说明．（参考数据：

3

≈1.7）

Answer 1

考点：二次根式的应用

专题：

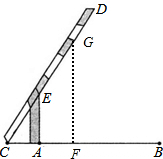
分析：首先在AB之间找一点F，且BF=2.5，过点F作GF⊥AB交CD于点G，只要求得GF的数值，进一步与货车高相比较得出答案即可．

解答：解：如图，

在AB之间找一点F，使BF=2.5m，过点F作GF⊥AB交CD于点G，
∵AB=3.2m，CA=0.7m，BF=2.5m，
∴CF=AB-BF+CA=1.4m，
∵∠ECA=60°，
∴tan60°=

GF

CA

，
∴GF=CAtan60°=1.4

3

≈2.38m，
∵2.38＜3
∴这辆货车在不碰杆的情况下，不能从入口内通过．

点评：此题考查二次根式的运用以及锐角三角函数的实际运用，理解题意，结合图形，选用适当的方法解决问题．