
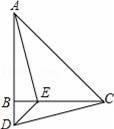
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

科目:初中数学 来源: 题型:
如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )

A.AB=2AE B.AC=2CD C.DB=2CD D.AD=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
一汽艇保持发动机功率不变,它在相距25千米的A,B两码头之间流动的河水中往返一次(其中汽艇的速度大于河水的速度)与它在平静的湖水中航行50千米比较,两次航行所用时间的关系是( )
A.在平静的湖水中用的时间少 B.在流动的河水中用的时间少
C.两种情况所用时间相等 D.以上均有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com