
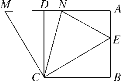
【题目】如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CE,CM.
(1)求证:∠BCE=∠DCM;
(2)若点N在边AD上,且∠NCE=45°,连接NC,NE,求证:NE=BE+DN;
(3)在(2)的条件下,若DN=2,MD=3,求正方形ABCD的边长.
【答案】(1)证明见解析;(2)证明见解析;(3)正方形ABCD的边长为6.
【解析】
(1)根据正方形的性质得到CD=BC,∠ADC=∠B=90°,
根据全等三角形的性质得到∠BCE=∠DCM;
(2)根据全等三角形的性质得到∠BCE=∠DCM,CE=CM,根据全等三角形的性质得到NE=MN,等量代换即可得到结论;
(3)设正方形的边长为x根据勾股定理即可得到结论.
(1)证明:在正方形ABCD中,
∵CD=BC,∠ADC=∠B=90°,
∴∠MDC=∠B=90°,
在△BCE与△CDM中,
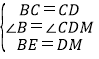 ,
,
∴△BCE≌△CDM,
∴∠BCE=∠DCM;
(2)∵∠NCE=45°,
∴∠BCE+∠DCN=45°,
∵△BCE≌△CDM,
∴∠BCE=∠DCM,CE=CM,
在△CEN与△CMN中,
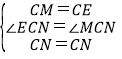 ,
,
∴△CEN≌△CMN,
∴NE=MN,
∵MN=MD+DN=BE+DN,
∴NE=BE+DN;
(3)设正方形的边长为x,
∵NE=BE+DN=MD+DN=3+2=5,AN=AD-DN=x-2,AE=x-3,
∵NE2=AN2+AE2,
∴52=(x-2)2+(x-3)2,
解得:x=6,或x=-1(不合题意,舍去),
∴正方形的边长是6.


科目:初中数学 来源: 题型:
【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)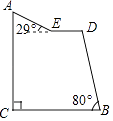
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:观察下面由“※”组成的图案和算式,解答问题:
1+3=4=(![]() )2=22
)2=22
1+3+5=9=(![]() )2=32
)2=32
1+3+5+7=16=(![]() )2=42
)2=42
…
问题解决:
(1)试猜想1+3+5+7+9…+49的结果为 ;
(2)若n 表示正整数,请用含n 的代数式表示1+3+5+7+9+…+(2n﹣1)+(2n+1) 的结果.
问题拓展:
(3)请用上述规律计算:1017+1019+…+2017+2019.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )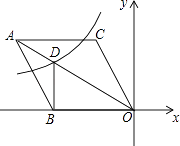
A.6 ![]()
B.﹣6 ![]()
C.12 ![]()
D.﹣12 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
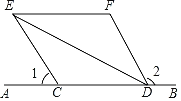
【题目】已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)求证:CE∥DF;
(2)若∠DCE=126°,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D是 ![]() 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F. 
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DFDB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.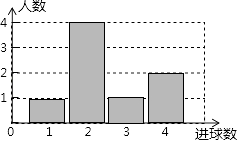
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com