
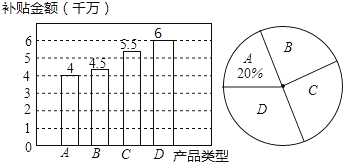
【题目】近几年来,国家对购买新能源汽车实行补助政策,2016年某省对新能源汽车中的“插电式混合动力汽车”实行每辆3万元的补助,小刘对该省2016年“纯电动乘用车”和“插电式混合动力车”的销售计划进行了研究,绘制出如图所示的两幅不完整的统计图.
(1)补全条形统计图;
(2)求出“D”所在扇形的圆心角的度数;
(3)为进一步落实该政策,该省计划再补助4.5千万元用于推广上述两大类产品,请你预测,该省16年计划大约共销售“插电式混合动力汽车”多少辆?
注:R为纯电动续航行驶里程,图中A表示“纯电动乘用车”(100km≤R<150km),B表示“纯电动乘用车”(150km≤R<250km),C表示“纯电动乘用车”(R≥250km),D为“插电式混合动力汽车”.
【答案】
(1)
解:补贴总金额为:4÷20%=20(千万元),
则D类产品补贴金额为:20﹣4﹣4.5﹣5.5=6(千万元),补全条形图如图:
(2)
解:360°× ![]() =108°,
=108°,
答:“D”所在扇形的圆心角的度数为108°
(3)
解:根据题意,16年补贴D类“插电式混合动力汽车”金额为:6+4.5× ![]() =7.35(千万元),
=7.35(千万元),
∴7350÷3=2450(辆),
答:预测该省16年计划大约共销售“插电式混合动力汽车”2450辆
【解析】(1)首先由A的数目和其所占的百分比可求出总数,进而可求出D的数目,问题得解;
(2)由D的数目先求出它所占的百分比,再用百分比乘以360°,即可解答;
(3)计算出补贴D类产品的总金额,再除以每辆车的补助可得车的数量.本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
【考点精析】解答此题的关键在于理解扇形统计图的相关知识,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况,以及对条形统计图的理解,了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】八年级(1)班有48名学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去动物园的学生数”的扇形圆心角为60°,则下列说法正确的是( )
A. 想去动物园的学生占全班学生的60% B. 想去动物园的学生有12人
C. 想去动物园的学生肯定最多 D. 想去动物园的学生占全班学生的![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )
A.4.5
B.6
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
R三点分别在CD、AD、BC上,如图所示.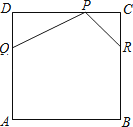
(1)当皮雕师傅切下△PDQ时,若DQ长度为x公分,请你以x表示此时△PDQ的面积.
(2)承(1),当x的值为多少时,五边形PQABR的面积最大?请完整说明你的理由并求出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为 ![]() ;④AD2+BE2﹣2OP2=2DPPE,其中所有正确结论的序号是
;④AD2+BE2﹣2OP2=2DPPE,其中所有正确结论的序号是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上两点A,B对应的数分别是﹣1,3,点P为数轴上的一动点,其对应的数为x

(1)A、B两点的距离AB= ;
(2)在数轴上是否存在点P,使PA+PB=6?若存在,请求出x的值;若不存在,请说明理由.
(3)如图2,若点P以每秒1个单位的速度从点O出发向右运动,同时点A以每秒5个单位的速度向左运动,点B以每秒20个单位的速度向右运动,在运动的过程中,M、N分别是AP、OB的中点,问:![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C在双曲线![]() 上,点 B、D在双曲线
上,点 B、D在双曲线![]() 上,AD// BC//y 轴.
上,AD// BC//y 轴.
(I)当m=6,n=-3,AD=3 时,求此时点 A 的坐标;
(II)若点A、C关于原点O对称,试判断四边形 ABCD的形状,并说明理由;
(III)若AD=3,BC=4,梯形ABCD的面积为![]() ,求mn 的最小值.
,求mn 的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com