
����Ŀ����ͼ���ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ������Ϊ��0��6������
��������0��6������![]() ��������4��0������
������Ϊ��4��0������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��2����λ���ȵ��ٶ����
��ÿ��2����λ���ȵ��ٶ����![]() ������ͬʱ��
������ͬʱ��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��3����λ���ȵ��ٶ����
��ÿ��3����λ���ȵ��ٶ����![]() �˶�������
�˶�������![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() ��
��![]() ͬʱֹͣ�˶������˶�ʱ��Ϊ
ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() �룮
�룮
��1����![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() �����Ϊ_____________��
�����Ϊ_____________��
��2����![]() ��
��![]() ����ʱ����
����ʱ����![]() ��ֵ��
��ֵ��
��3��������������![]() ��ͼ����
��ͼ����![]() ��
��![]() ����ʱ��
����ʱ��
����![]() ��ֵ��
��ֵ��
�ڵ�![]() ��
��![]() ���ϣ���
���ϣ���![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ����Ե�
��ͼ���ϣ����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ���ֱ��д����������������
Ϊ������ı�����ƽ���ı��Σ���ֱ��д����������������![]() �����꣮
�����꣮

���𰸡���1��3����2��![]() ��
��![]() ����3����
����3����![]() ����
����![]()
��������
��1��BP=4-2t��BQ=3t����t=1���������������������ʽ��ü���.
��2����![]() ʱ�����֢�
ʱ�����֢�![]() ����
����![]() ����������.
����������.
��3���ٽ�![]() ��
��![]() ����
����![]() ���ɵ�k.�ڸ���ƽ���ı��ε����ʣ�P��Q�����������IJ����M��N��������IJ���췽�����
���ɵ�k.�ڸ���ƽ���ı��ε����ʣ�P��Q�����������IJ����M��N��������IJ���췽�����
�⣺��1��BP=4-2t��BQ=3t����t=1ʱ�����������Ϊ![]() =3.
=3.
��2���ٵ�![]() ʱ����
ʱ����![]()
��![]() ��
��![]() ��
��![]()
![]()
��![]()
�ڵ�![]() ʱ����
ʱ����![]()
��![]() ��
��![]()
��![]() ��
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
���ϣ�![]() ��
��![]()
��3���١�![]() ��
��![]()
�� ��
��![]() ��
��![]()
��
���ݢ���k=12,t=1,P(2,6),Q(4,3)
��M������Ϊ(x,0),N(a,![]() )
)
����ƽ���ı��ε����ʣ�P��Q�����������IJ����M��N��������IJ���췽����⣬
x-4=2-a,3=![]() -6,
-6,
���a=![]() ,x=
,x=![]() .
.
����M������Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A���ʾ��a��B���ʾ��b��C���ʾ��C��b����С������������a����2��c��7��
��1�����������۵���ʹ��A����C���غϣ����B������ ����ʾ�ĵ��غϣ�
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������t���ӹ�������A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC��
��AB���� ����AC���� ����BC���� �������ú�t�Ĵ���ʽ��ʾ��
��3�����ʣ�3BC��2AB��ֵ�Ƿ�����ʱ��ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǽ���ͼ��ʾ������������ʽ�ĵ�ĸ����ֱ����������������(��1��3��6��10��)��������������(��1��4��9��16��)����С��200�����У�������������������Ϊm������������������Ϊn����m+n��ֵΪ��_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AC=1cm��BC=2cm����P�ӵ�A��������1cm/s���ٶ�������AC��CB��BA�˶������ջص���A�����P���˶�ʱ��Ϊx��s�����߶�AP�ij���Ϊy��cm�������ܹ���ӳy��x֮�亯����ϵ��ͼ������ǣ� ��

A.  B.
B. 
C. 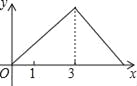 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɳ��ijѧУ�����꼶���ְ༶�����ǻۿ����Ե㣬һ����������ѧ�����ҳ�������ѧУ���������ڸ���༶�����ƹ㣬���ǵ�ƽ�������ʧ�������ѧУ�����ɹ�![]() ̨ƽ����Ժ�һ��ƽ���(ƽ���֧������
̨ƽ����Ժ�һ��ƽ���(ƽ���֧������![]() ֧).�ִ�
֧).�ִ�![]() ��
��![]() ���ҹ�˾�˽��ƽ����Լ۸���ÿ̨
���ҹ�˾�˽��ƽ����Լ۸���ÿ̨![]() Ԫ��ƽ���ÿ֧
Ԫ��ƽ���ÿ֧![]() Ԫ.
Ԫ.![]() ��˾���Ż�����Ϊÿ̨ƽ���������
��˾���Ż�����Ϊÿ̨ƽ���������![]() ֧ƽ��ʣ�
֧ƽ��ʣ�![]() ��˾���Ż�����Ϊ������Ŀ�������.
��˾���Ż�����Ϊ������Ŀ�������.
(1)����ѧУ��Ҫ����ƽ���![]() ֧���ú�
֧���ú�![]() �Ĵ���ʽ�ֱ��ʾ���ҹ�˾���ܷ���
�Ĵ���ʽ�ֱ��ʾ���ҹ�˾���ܷ���![]() ��
��![]() ��
��
(2)��ѧУȷ������![]() ̨ƽ����Ժ�
̨ƽ����Ժ�![]() ֧ƽ��������ҹ�˾��������ѡ������Ϊ������Ҫ���Ѷ��٣��������˵��.
֧ƽ��������ҹ�˾��������ѡ������Ϊ������Ҫ���Ѷ��٣��������˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��4��0����C��8��0����D��8��8��.������y=ax2+bx��A��C����.
(1)ֱ��д����A�����꣬����������ߵĽ���ʽ��
(2)����P�ӵ�A���������߶�AB���յ�B�˶���ͬʱ��Q�ӵ�C���������߶�CD���յ�D�˶����ٶȾ�Ϊÿ��1����λ���ȣ��˶�ʱ��Ϊt��.����P��PE��AB��AC�ڵ�E
������E��EF��AD�ڵ�F�����������ڵ�G.��tΪ��ֵʱ���߶�EG�?
������EQ���ڵ�P��Q�˶��Ĺ����У��ж��м���ʱ��ʹ����CEQ�ǵ���������?��ֱ��д����Ӧ��tֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OC��OB��OD��������ۣ��١�AOB=��COD���ڡ�AOB+��COD=90�����ۡ�BOC+��AOD=180�����ܡ�AOC����COD=��BOC�У���ȷ����________������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺��1��29��(��8)��![]()
��2��(��3)��![]()
��3����60��![]()
��4��(��1)2019��|(��2)3��10|��(��22)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A���ʾ��a��B���ʾ��b��a��b����|a+2|+|b��4|��0��
��1����A��ʾ����Ϊ�� ������B��ʾ����Ϊ�� ����
��2��һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶������˶���ʱ��Ϊt���룩��
����t��1ʱ����С��ԭ��ľ���Ϊ�� ������С��ԭ��ľ���Ϊ�� ������t��3ʱ����С��ԭ��ľ���Ϊ�� ������С��ԭ��ľ���Ϊ�� ����
����̽�����ף�����С��ԭ��ľ����������������ܣ���˵�����ɣ����ܣ�������ף�����С��ԭ��ľ������ʱ������ʱ�䣮
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com