
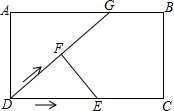
 如图所示,在矩形ABCD中,AB=5cm,AD=3cm,G为边AB上一点,GB=1cm,动点E、F同时从点D出发,点F沿射线DG-GB-BC运动到点C时停止,点E沿DC运动到点C时停止,它们运动的速度都是1cm/s,若E、F同时运动t s时,△DEF的面积为5cm2,则t的值为$\frac{5\sqrt{6}}{3}$或7.
如图所示,在矩形ABCD中,AB=5cm,AD=3cm,G为边AB上一点,GB=1cm,动点E、F同时从点D出发,点F沿射线DG-GB-BC运动到点C时停止,点E沿DC运动到点C时停止,它们运动的速度都是1cm/s,若E、F同时运动t s时,△DEF的面积为5cm2,则t的值为$\frac{5\sqrt{6}}{3}$或7. 分析 分三种情况:①点F在DG上;②点F在BG上;③点F在BC上;根据等量关系:△DEF的面积为5cm2,列出方程求解即可.
解答 解:在Rt△ADG中,DG=$\sqrt{{3}^{2}+(5-1)^{2}}$=5,
①点F在DG上,依题意有
$\frac{1}{2}$t×$\frac{3}{5}$t=5,
解得t=±$\frac{5\sqrt{6}}{3}$(负值舍去);
②点F在BG上,依题意有
$\frac{1}{2}$×5×3≠5,
此种情况不存在,
③点F在BC上,依题意有
$\frac{1}{2}$×5×[3-(t-6)]=5,
解得t=7.
答:t的值为$\frac{5\sqrt{6}}{3}$或7.
故答案为:$\frac{5\sqrt{6}}{3}$或7.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知圆O,
已知圆O,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 62 | B. | 35 | C. | 33 | D. | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8,9 | B. | 9,8.5 | C. | 8.5,9 | D. | 8,8.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(公里) | 80 | 120 | 180 | 200 | … |
| y(元) | 200 | 300 | 450 | 500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com