
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣ ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.

(1)①(0,2)或(0,﹣2) ②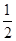
(2)①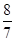 C(﹣
C(﹣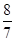 ,
,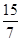 ) ②E(﹣
) ②E(﹣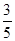 ,
,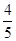 ),C(﹣
),C(﹣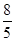 ,
,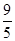 ),1
),1
【解析】【解析】
(1)①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|﹣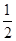 ﹣0|=
﹣0|=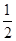 ≠2,
≠2,
∴|0﹣y|=2,
解得,y=2或y=﹣2;
∴点B的坐标是(0,2)或(0,﹣2);
②点A与点B的“非常距离”的最小值为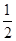
(2)①如图2,
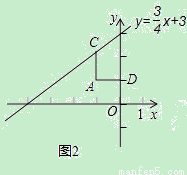
取点C与点D的“非常距离”的最小值时,需要根据运算定义“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”解答,此时|x1﹣x2|=|y1﹣y2|.即AC=AD,
∵C是直线y=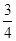 x+3上的一个动点,点D的坐标是(0,1),
x+3上的一个动点,点D的坐标是(0,1),
∴设点C的坐标为(x0,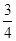 x0+3),
x0+3),
∴﹣x0=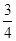 x0+2,
x0+2,
此时,x0=﹣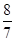 ,
,
∴点C与点D的“非常距离”的最小值为:|x0|=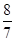 ,
,
此时C(﹣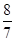 ,
,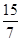 );
);
②如图3
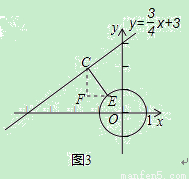
当点E在过原点且与直线y=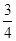 x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则
x+3垂直的直线上时,点C与点E的“非常距离”最小,设E(x,y)(点E位于第二象限).则
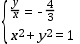 ,
,
解得,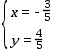 ,
,
故E(﹣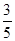 ,
,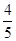 ).
).
﹣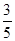 ﹣x0=
﹣x0=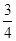 x0+3﹣
x0+3﹣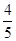 ,
,
解得,x0=﹣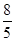 ,
,
则点C的坐标为(﹣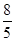 ,
,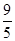 ),
),
最小值为1.
(1)①根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0﹣y|=2,据此可以求得y的值;
②设点B的坐标为(0,y),因为|﹣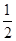 ﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣
﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣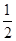 ﹣0|=
﹣0|=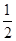 ;
;
(2)①设点C的坐标为(x0,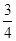 x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0=
x0+3),根据材料“若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|”可知,C、D两点的“非常距离”的最小值为﹣x0=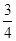 x0+2,据此可以求得点C的坐标;
x0+2,据此可以求得点C的坐标;
②当点E在过原点且与直线y=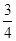 x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣
x+3垂直的直线上时,点C与点E的“非常距离”最小,即E(﹣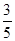 ,
,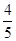 ).解答思路同上.
).解答思路同上.


科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:选择题
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
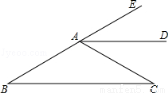
A.30° B.60° C.80° D.120°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学概率(解析版) 题型:解答题
“五一”假期,某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
(1)若去丁地的车票占全部车票的10%,请求出去丁地的车票数量,并补全统计图(如图所示).
(2)若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张(所有车票的形状、大小、质地完全相同、均匀),那么员工小胡抽到去甲地的车票的概率是多少?
(3)若有一张车票,小王和小李都想去,决定采取摸球的方式确定,具体规则:“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球(球除数字不同外完全相同),并放回让另一人摸,若小王摸得的数字比小李的小,车票给小王,否则给小李.”试用列表法或画树状图的方法分析这个规则对双方是否公平?

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学整体思想(解析版) 题型:选择题
如图,正方形ABCD的边长为6cm,O是AB的中点,也是抛物线的顶点,OP⊥AB,两半圆的直径分别为OA,OB,抛物线经过C,D两点,且关于OP对称,则图中阴影部分的面积为( )(π取3.14,结果保留两位小数)

A.7.07cm2
B.3.53cm2
C.14.13cm2
D.10.60cm2
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:解答题
已知a、b是正实数,那么,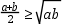 是恒成立的.
是恒成立的.
(1)由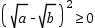 恒成立,说明
恒成立,说明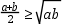 恒成立;
恒成立;
(2)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明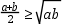 恒成立.
恒成立.
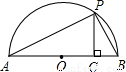
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学尺规作图(解析版) 题型:选择题
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中不正确的是( )

A.AD是∠BAC的平分线 B.∠ADC=60°
C.点D在AB的中垂线上 D.S△DAC:S△ABD=1:3
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )

A.当弦PB最长时,△APC是等腰三角形
B.当△APC是等腰三角形时,PO⊥AC
C.当PO⊥AC时,∠ACP=30°
D.当∠ACP=30°时,△BPC是直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com