
“五一”假期,某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
(1)若去丁地的车票占全部车票的10%,请求出去丁地的车票数量,并补全统计图(如图所示).
(2)若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张(所有车票的形状、大小、质地完全相同、均匀),那么员工小胡抽到去甲地的车票的概率是多少?
(3)若有一张车票,小王和小李都想去,决定采取摸球的方式确定,具体规则:“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球(球除数字不同外完全相同),并放回让另一人摸,若小王摸得的数字比小李的小,车票给小王,否则给小李.”试用列表法或画树状图的方法分析这个规则对双方是否公平?

(1)10 图见解析 (2)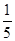 (3)不公平
(3)不公平
【解析】【解析】
(1)根据题意得:(20+40+30)÷(1﹣10%)=100(张),
则D地车票数为100﹣(20+40+30)=10(张),补全图形,如图所示:
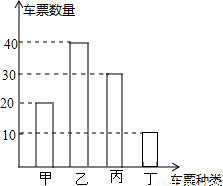
(2)总票数为100张,甲地票数为20张,
则员工小胡抽到去甲地的车票的概率为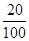 =
=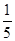 ;
;
(3)列表如下:
| 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
所有等可能的情况数有16种,其中小王掷得数字比小李掷得的数字小的有6种:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),
∴P小王掷得的数字比小李小=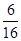 =
=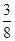 ,
,
则P小王掷得的数字不小于小李=1﹣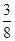 =
=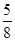 ,
,
则这个规则不公平.
(1)根据丁地车票的百分比求出甲,乙,丙地车票所占的百分比之和,用甲,乙,丙车票之和除以百分比求出总票数,得出丁车票的数量,补全条形统计图即可;
(2)根据甲,乙,丙,丁车票总数,与甲地车票数为20张,即可求出所求的概率;
(3)列表得出所有等可能的情况数,求出两人获胜概率,比较即可得到公平与否.


科目:初中数学 来源:2014中考名师推荐数学解直角三角形(解析版) 题型:选择题
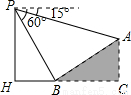
如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
A.15 B. C.
C.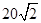 D.
D.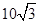
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学立体图形(解析版) 题型:选择题
如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. B.25 C.
B.25 C.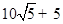 D.35
D.35
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学模型思想(解析版) 题型:解答题
许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表:
旋钮角度(度) | 20 | 50 | 70 | 80 | 90 |
所用燃气量(升) | 73 | 67 | 83 | 97 | 115 |
(1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由,并求出它的解析式;
(2)当旋钮角度为多少时,烧开一壶水所用燃气量最少?最少是多少?
(3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭以前每月的平均燃气量.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学展示定义、规则(解析版) 题型:解答题
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣ ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的规律(解析版) 题型:填空题
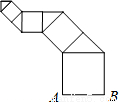
按如图方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2,…,则第n个正方形与第n个等腰直角三角形的面积和Sn= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com