
【题目】已知抛物线![]() 经过坐标原点O,与x轴交于另一点A,顶点为B.求:
经过坐标原点O,与x轴交于另一点A,顶点为B.求:
(1)抛物线的解析式;
(2)△AOB的面积;
(3)要使二次函数的图象过点(10,0),应把图象沿x轴向右平移 个单位
【答案】(1)![]() ;(2)8;(3)图象沿x轴向右平移6或10 个单位.
;(2)8;(3)图象沿x轴向右平移6或10 个单位.
【解析】
(1)根据题意,得到n+1=0,求得n的值,即可求出抛物线解析式;
(2)将抛物线解析式化为顶点式求顶点B坐标,再求抛物线与x轴交点,即可求得△AOB的面积;
(3)根据(2)中求得的抛物线与x轴交点的坐标,再结合平移即可解答.
(1) ∵抛物线![]() 经过坐标原点O
经过坐标原点O
∴n+1=0,n=﹣1,
∴抛物线解析式为:![]()
(2)![]() ,∴顶点B的坐标(2,-4);
,∴顶点B的坐标(2,-4);
抛物线![]() 与x轴交点为(4,0)(0,0)
与x轴交点为(4,0)(0,0)
∴点A的坐标(4,0)
所以△AOB的面积是![]()
(3)抛物线![]() 与x轴交点为(4,0)(0,0)
与x轴交点为(4,0)(0,0)
∴将图象沿x轴向右平移6或10 个单位,二次函数的图象过点(10,0)
故答案为:6或10


科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上.

(1)从中随机抽出一张牌,牌面数字是奇数的概率是 ;
(2)从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,AC是对角线,E是平面内一点,且![]() ,过点C作
,过点C作![]() ,且
,且![]() 。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
。连接AE、AF,M是AF的中点,作射线DM交AE于点N.
(1)如图1,若点E,F分别在BC,CD边上。
求证:①![]() ;
;
②![]() ;
;
(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求![]() 与
与![]() 的和的度数。
的和的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
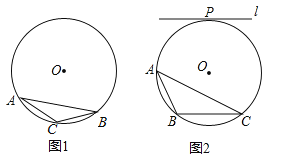
(1)如图1,AC=BC;
(2)如图2,直线l与⊙O相切于点P,且l∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E在边CD上,连结AE并延长与BC的延长线交于点F.
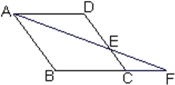
(1)写出图中所有的相似三角形(不需证明);
(2)若菱形ABCD的边长为6,DE:AB=3:5,试求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣bx+c的y与x的部分对立值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论①抛物线的开口向下:②其图象的对称轴为x=1:③当x<1时.函数值y随x的增大而增大,④方程ax2+bx+c=0有一个根大于4.其中正确的结论有_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年北疆承办了世界园艺博览会,某商店为了抓住博览会的商机,决定购买A.B两种世园会纪念品,若购进A中纪念品20件,B种纪念品10件,需要2000元;若购进A中纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A.B两种纪念品每件各需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种的6倍,且少于B种纪念品数量的8倍,设购进B种纪念品a件,则该商店共有几种进货方案?
(3)在第(2)问的条件下,若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润40元,设总利润为y元,请写出总利润y(元)与a(个)的函数关系式,并根据函数关系式说明总利润最高时的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
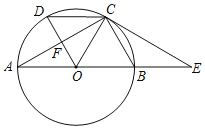
【题目】AB是⊙O的直径,C点在⊙O上,F是AC的中点,OF的延长线交⊙O于点D,点E在AB的延长线上,∠A=∠BCE.
(1)求证:CE是⊙O的切线;
(2)若BC=BE,判定四边形OBCD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com