
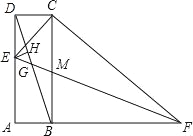
【题目】如图,已知在矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连结BD,过点E作EH⊥BD,垂足为H,连结EF,交BD于点G,交BC于点M,连结CF.
(1)△CDE与△CBF相似吗?为什么?
(2)求证:∠DBC=∠EFC;
(3)同线段GH的值是定值吗?如果不是,请说明理由;如果是,求出这个定值.
【答案】(1)答案见解析 (2)证明见解析 (3)是定值 ![]()
【解析】
(1)根据两边成比例夹角相等两三角形相似即可判断;
(2)想办法证明△DCB∽△ECF,可得∠DBC=∠EFC;
(3)结论:线段GH的值是定值.GH=![]() .由△EDC∽△EHG,可得
.由△EDC∽△EHG,可得![]() =
=![]() ,由AB=DC,可得
,由AB=DC,可得![]() =
=![]() ,想办法用t表示EH,代入化简即可解决问题.
,想办法用t表示EH,代入化简即可解决问题.
(1)∵四边形ABCD是矩形,AD∥BC,AB=DC,
∴∠CDA=∠DCB=∠DAB=∠ABC=90°,
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠CDE=∠FBC=90°
∴△CDE∽△CBF;
(2)证明:∵△CDE∽△CBF,
∴∠DCE=∠BCF,![]() =
=![]() ,
,
∵∠DCE+∠BCE=90°,
∴∠BCE+∠BCF=90°,
∴∠ECF=90°,
∴![]() =
=![]() ,
,
∵∠DCB=∠ECF
∴△DCB∽△ECF,
∴∠DBC=∠EFC.
(3)结论:线段GH的值是定值.GH=![]() .
.
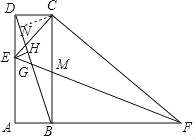
理由:作CN⊥DB于N,
∵AD=BC=6,AB=2,
∴BD=![]() =2
=2![]() ,
,
∵∠EDH=∠ADB,∠EHD=∠DAB,
∴△DEH∽△DBA,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴EH=![]() t,
t,
∵△DCB∽△ECF,
∴∠DBC=∠EFC,
∴∠CDB=∠CEF,
∵∠CDB+∠DCN=90°,∠DCN+∠NCB=90°,
∴∠BDC=∠NCB=∠CEF
∵CN⊥BD,EH⊥DB,
∴CN∥EH,
∴∠NCE=∠CEH,
∴∠ECB=∠HEG,
∵AD∥BC,
∴∠DEC=∠ECB,
∴∠DEC=∠HEG,
∵∠EDC=∠EHG=90°,
∴△EDC∽△EHG,
∴![]() ,
,
∵AB=DC,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴HG=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=(m+1)x+4的图像与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为4.
(1)则![]() = 及点
= 及点![]() 的坐标为( );
的坐标为( );
(2)过点B作直线BP与![]() 轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;
轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;
(3)将一次函数![]() 的图像绕点B顺时针旋转
的图像绕点B顺时针旋转![]() , 求旋转后的对应的函数表达式.
, 求旋转后的对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
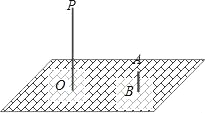
【题目】如图,晚上,小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )

A. ![]() 米 B. 2米 C. 2
米 B. 2米 C. 2![]() 米 D. 3米
米 D. 3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
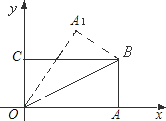
(A).(4.8,6.4) (B).(4,6) (C)(5.4,5.8) (D).(5,6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com