
【题目】如图,一次函数y=(m+1)x+4的图像与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为4.
(1)则![]() = 及点
= 及点![]() 的坐标为( );
的坐标为( );
(2)过点B作直线BP与![]() 轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;
轴的正半轴相交于点P,且OP=4OA,求直线BP的解析式;
(3)将一次函数![]() 的图像绕点B顺时针旋转
的图像绕点B顺时针旋转![]() , 求旋转后的对应的函数表达式.
, 求旋转后的对应的函数表达式.

【答案】(1)1,(-2,0);(2)![]() ;(3)
;(3)![]()
【解析】
(1)先求得OB=4,然后根据三角形面积求得OA的长,即可求得A的坐标,把A的坐标代入y=(m+1)x+4,即可求得m的值;
(2)利用OP=4OA=8可得到点P的坐标为(8,0),然后利用待定系数法求直线BP的函数解析式.
(3)直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转 ![]() 的直线交
的直线交![]() 轴于
轴于![]() 点,过点
点,过点![]() 于点
于点![]() ,作
,作![]() 轴.根据容易证明
轴.根据容易证明![]() ,确定F点的坐标
,确定F点的坐标
解:(1)∵直线y=(m+1)x+4与y轴的交点B(0,4),∴OB=4,
∵S△OAB=4,
∴![]() ×OA×OB=4,
×OA×OB=4,
∴OA=2,∴A(-2,0),
把点A(-2,0)代入y=(m+1)x+4,得-2(m+1)+4=0,
解得m=1;
故答案为1,(-2,0);
(2)![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入得
代入得![]() ,
,
直线![]() 的解析式为
的解析式为![]() ;
;
( 3)直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转 ![]() 的直线交
的直线交![]() 轴于
轴于![]() 点,过点
点,过点![]() 于点
于点![]() ,作
,作![]() 轴,
轴,

∵直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转 ![]()
∴∠ABE=![]() ,
,
∵![]() ,
,
∴∠BAF=![]()
∴AF=AB, ∠BAO+∠FAE=![]()
∵![]() 轴, ∠AOB=
轴, ∠AOB=![]()
∴∠FHA=∠AOB=![]() , ∠ABO+∠BAO=
, ∠ABO+∠BAO=![]()
∴∠FAE=∠ABO
在![]() 中
中

∴![]()
FH=OA=2, HA=OB=4
![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
 ,
,
直线![]() 的解析式为
的解析式为![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
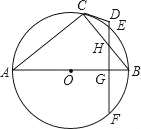
【题目】如图,已知AB是⊙O的直径,BC、EF是⊙O的弦,且EF垂直AB于点G,交BC于点H,CD与FE延长线交于D点,CD=DH.
(1)求证:CD是⊙O的切线;
(2)若H为BC中点,AB=10,EF=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
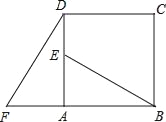
【题目】如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
查看答案和解析>>
科目:初中数学 来源: 题型:
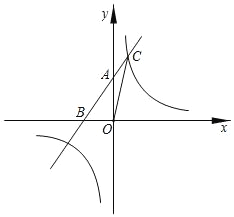
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
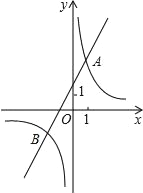
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
(1)分别求出这两个函数的关系式;
(2)观察图象,直接写出关于x的不等式![]() ﹣ax﹣b>0的解集;
﹣ax﹣b>0的解集;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B是反比例函数y=![]() (k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )

A. ﹣12 B. ﹣10 C. ﹣9 D. ﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
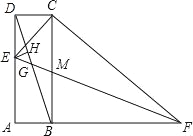
【题目】如图,已知在矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连结BD,过点E作EH⊥BD,垂足为H,连结EF,交BD于点G,交BC于点M,连结CF.
(1)△CDE与△CBF相似吗?为什么?
(2)求证:∠DBC=∠EFC;
(3)同线段GH的值是定值吗?如果不是,请说明理由;如果是,求出这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】田忌赛马的故事为我们所熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块l0、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取一张牌进行比较,数字大的为本“局”获胜,每次取的牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出l0时,小齐随机出牌应对,求小齐本次比赛获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com