
【题目】如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(﹣1,0),点D的坐标为(1,6). 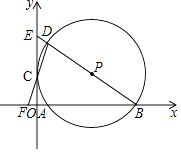
(1)求证:CD=CF;
(2)判断⊙P与y轴的位置关系,并说明理由;
(3)求直线BD的解析式.
【答案】
(1)解:如图,作DH⊥OE于点H,
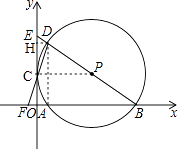
∴∠DHC=∠FOC=90°,∠DCH=∠FCO,
∵D(1,6)、F(﹣1,0),
∴DH=OF=1,
在△COF和△CHD中,
∵ 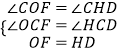 ,
,
∴△COF≌△CHD(AAS),
∴CD=CF
(2)解:连接PC,

∵CD=CF、PD=PB,
∴PC为△BDF的中位线,
∴PC∥BF,
∵BF⊥y轴,
∴PC⊥y轴,
又PC为⊙P的半径,
∴⊙P与y轴相切
(3)解:如图,连接AD,

由(2)知BF=2PC,
∵BD=2PC,
∴BD=BF,
∵BD是⊙P的直径,
∴∠DAB=90°,
∴AD=OH=6,OA=DH=1,
设BD=x,
则AB=x﹣2,
由BD2=AB2+AD2得x2=(x﹣2)2+62,
解得:x=10,
∴OB=OA+AB=1+8=9,即B(9,0),
设直线BD的解析式为y=kx+b,
把B(9,0)、D(1,6)代入得 ![]() ,
,
解得: 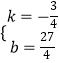 ,
,
∴直线BD的解析式为y=﹣ ![]() x+
x+ ![]()
【解析】(1)证△COF≌△CHD可得CD=CF;(2)连接PC,先由CD=CF、PD=PB知PC∥BF,结合BF⊥y轴知PC⊥y轴,即可得出结论;(3)连接AD,证BD=BF可得AD=OH=6、OA=DH=1,设BD=x,由BD2=AB2+AD2得x=10,从而知B(9,0),待定系数法求解可得.


科目:初中数学 来源: 题型:
【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( ) 
A.1元
B.2元
C.3元
D.4元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a+b=1,ab=-1.设![]()
(1)计算S2;
(2)请阅读下面计算S3的过程: ![]()
=![]()
=![]()
=![]()
∵a+b=1,ab=-1,
∴![]() _______.
_______.
你读懂了吗?请你先填空完成(2)中S3的计算结果;再计算S4;
(3)猜想并写出![]() ,
, ![]() ,
, ![]() 三者之间的数量关系(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S3.
三者之间的数量关系(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)、B(3,0)两点,与y轴交于点C(0,3).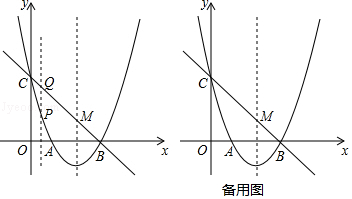
(1)求抛物线的解析式;
(2)设点P是位于直线BC下方的抛物线上一动点,过点P作y轴的平行线交直线BC于点Q,求线段PQ的最大值;
(3)在(2)的条件下,抛物线的对称轴与直线BC交于点M,问是否存在点P,使以M、P、Q为顶点的三角形与△CBO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com