
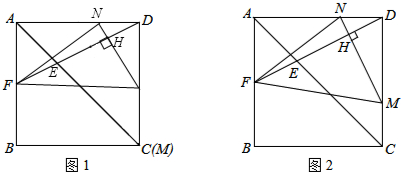
分析 (1)①过E作EG⊥AB于点H,可知EG=t,AF=2,FG=2-t,由平行线分线段成比例可得$\frac{EG}{AD}$=$\frac{FG}{AF}$,可求得t的值;②当t=$\frac{4}{3}$时,在Rt△EFG、Rt△AFD、△DMN中可分别求得EF、FD、DH,可求得EH,可求得答案;
(2)可先证明△AFE∽△CDE,可用t表示出AF,再证明△MND∽△DFA,可求得ND=t,可证明ND=CM;当△MNF为等腰三角形,可分三种情况,即FN=MN、FN=FM和FM=MN,再结合等腰三角形的性质可分别求得满足条件的t的值.
解答 (1)解:①如图1,过E作EG⊥AB于点G,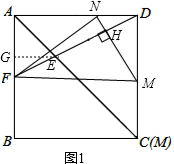
当F为AB中点时,则AF=$\frac{1}{2}$AB=2,
∵四边形ABCD为正方形,
∴∠BAC=45°,
∵AE=$\sqrt{2}$t,
∴AG=GE=t,
∴GF=AF-AG=2-t,
又GE∥AD,
∴$\frac{GE}{AD}$=$\frac{FG}{FA}$,即$\frac{t}{4}$=$\frac{2-t}{t}$,解得t=$\frac{4}{3}$,
即当t为$\frac{4}{3}$时,F为AB的中点;
②由①可知当F为AB中点时,t=$\frac{4}{3}$,
则GF=2-t=2-$\frac{4}{3}$=$\frac{2}{3}$,在Rt△EFG中,可求得EF=$\frac{2\sqrt{5}}{3}$,
在Rt△ADF中,AD=4,AF=2,可求得DF=2$\sqrt{5}$,
∵DF⊥MN,
∴∠DNM+∠ADF=∠AFD+∠ADF=90°,
∴∠DNM=∠AFD,且∠FAD=∠NDM,
∴△DMN∽△ANF,
∴$\frac{DM}{DN}$=$\frac{AD}{AF}$,
∵CM=t,
∴DM=4-t=4-$\frac{4}{3}$=$\frac{8}{3}$,
∴$\frac{\frac{8}{3}}{DN}$=$\frac{4}{2}$,解得DN=$\frac{4}{3}$,在Rt△DMN中,可求得MN=$\frac{4\sqrt{5}}{3}$,
又由面积相等可得DM•DN=MN•DH,即$\frac{8}{3}$×$\frac{4}{3}$=$\frac{4}{3}$$\sqrt{5}$•DH,解得DH=$\frac{8\sqrt{5}}{15}$,
∴EH=DF-EF-DH=2$\sqrt{5}$-$\frac{2\sqrt{5}}{3}$-$\frac{8\sqrt{5}}{15}$=$\frac{4\sqrt{5}}{5}$,
∴DH:HE:EF=$\frac{8\sqrt{5}}{15}$:$\frac{4\sqrt{5}}{5}$:$\frac{2\sqrt{5}}{3}$=8:12:10=4:6:5,
故答案为:4;6;5;
(2)证明:∵AB∥CD,
∴△AFE∽△CDE,
∴$\frac{AF}{CD}$=$\frac{AE}{EC}$,即$\frac{AF}{4}$=$\frac{\sqrt{2}t}{4\sqrt{2}-\sqrt{2}t}$=$\frac{t}{4-t}$,解得AF=$\frac{4t}{4-t}$,
又由(1)可知△MND∽△DFA,
∴$\frac{ND}{AF}$=$\frac{MD}{AD}$,即$\frac{MD}{\frac{4t}{4-t}}$=$\frac{4-t}{4}$,解得MD=t,
∴DN=CM=t;
若△MNF为等腰三角形,则有三种情况:
①若FN=MN,则由AN=DM可知△FAN≌△NDM,
∴AF=ND,即$\frac{4t}{4-t}$=t,解得t=0,不合题意;
②若FN=FM,由MN⊥HM知,HN=HM,
∴DN=DM=MC,
∴t=2,此时点F与点B重合;
③若FM=MN,显然此时点F在BC边上,如图2,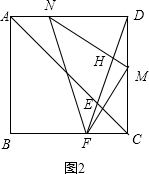
∵AN=DM,AD=CD,
∴ND=CM,
在△MFC和△NMD中
$\left\{\begin{array}{l}{MC=ND}\\{∠MCF=∠NDM}\\{MF=MN}\end{array}\right.$
∴△MFC≌△NMD(SAS),
∴FC=DM=4-t,
又可证得△NDM∽△DCF,
∴$\frac{DN}{DM}$=$\frac{DC}{FC}$,即$\frac{t}{4-t}$=$\frac{4}{FC}$,
∴FC=$\frac{4(4-t)}{t}$,
∴$\frac{4(4-t)}{t}$=4-t,解得t=4,此时点F与点C重合,
综上可知,当t=2或t=4时,△MNF能够成为等腰三角形,
故答案为:2或4.
点评 本题主要考查正方形的性质和相似三角形、全等三角形的判定和性质、等腰三角形的性质等知识点的综合应用.在(1)中把线段用t表示出来,利用相似求得t的值是解题的关键,在(2)中求得AF和CM的值是解题的关键.本题知识点较多,综合性较强,有一定的难度,且有一定的计算量.在解题时注意方程思想、分类讨论思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | (-1,$\frac{2}{3}$) | B. | (-2,$\frac{1}{3}$) | C. | (1,-$\frac{2}{3}$) | D. | (-$\frac{1}{3}$,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
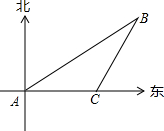 如图,在东西方向的海岸线一观测点A处,某时刻测得一艘匀速直线航行的渔船位于A的东偏北30°方向,且与点A相距20$\sqrt{3}$千米的B处,经过40分钟,该渔船在与A相距20千米的C处靠岸,求该渔船航行的速度.
如图,在东西方向的海岸线一观测点A处,某时刻测得一艘匀速直线航行的渔船位于A的东偏北30°方向,且与点A相距20$\sqrt{3}$千米的B处,经过40分钟,该渔船在与A相距20千米的C处靠岸,求该渔船航行的速度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
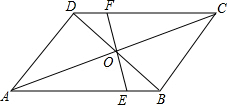 如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F、AB=4,AD=3,OF=1.3,求四边形BCFE的周长.
如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F、AB=4,AD=3,OF=1.3,求四边形BCFE的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
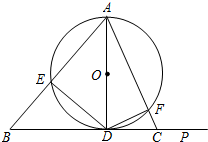 如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF.
如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
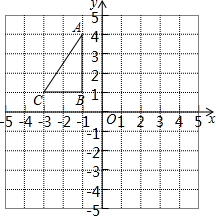 如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com