
【题目】如图,已知直线![]() ,点
,点![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 在点
在点![]() 的右侧,
的右侧,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() .
.

(1)写出![]() 的度数 ;
的度数 ;
(2)试求![]() 的度数(用含n的代数式表示);
的度数(用含n的代数式表示);
(3)将线段![]() 向右平行移动,使点
向右平行移动,使点![]() 在点
在点![]() 的右侧,其他条件不变,请画出图形并直接写出
的右侧,其他条件不变,请画出图形并直接写出![]() 的度数(用含n的代数式表示).
的度数(用含n的代数式表示).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() ,见解析.
,见解析.
【解析】
(1)根据角平分线的定义,即可得到∠EDC=![]() ∠ADC;
∠ADC;
(2)过点E作EF//AB,根据两直线平行,内错角相等可得∠ABE=∠BEF,∠CDE=∠DEF,根据角平分线的定义求出∠ABE,∠CDE,然后求解即可;
(3)过点E作EF//AB,然后分类讨论:①点A在点B的左边,根据角平分线的定义求出∠ABE,∠CDE,根据两直线平行,内错角相等可得∠ABF=∠BEF,∠CDE=∠DEF,然后求解;②点A在点B的右边时,根据角平分线的定义求出∠ABE,∠CDE,根据两直线平行,内错角相等可得∠CDE=∠DEF,根据两直线平行,同旁内角互补求出∠BEF,然后求解即可.
解:(1)![]() 平分
平分![]() ,
,![]() ,
,
![]() ;
;
(2)如图1,过点![]() 作
作![]() ,
,

![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)过点![]() 作
作![]() ,
,
①如图1,点![]() 在点
在点![]() 的右边时,同(2)可得,
的右边时,同(2)可得,![]() 不变,为
不变,为![]() ;
;
②如图2,点![]() 在点
在点![]() 的左边时,若点
的左边时,若点![]() 在直线
在直线![]() 和
和![]() 之间,则
之间,则
![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
若点![]() 在直线
在直线![]() 的上方或
的上方或![]() 的下方,则
的下方,则![]() ,
,
综上所述,![]() 的度数变化,度数为
的度数变化,度数为![]() 或
或![]() 或
或![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】(1)如果![]() +(n+6)2=0,求(m+n)2008+m3的值
+(n+6)2=0,求(m+n)2008+m3的值
(2)已知实数a,b,c,d,e,且ab互为倒数,c,d互为相反数,e的绝对值为2,求![]() ×ab+
×ab+![]() +e的值
+e的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,(在弹性限度![]() 内)已知一弹簧的长度
内)已知一弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系如下表:
之间的关系如下表:
物体的质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(1)当物体的质量为![]() 时,弹簧的长度是多少?
时,弹簧的长度是多少?
(2)如果物体的质量为![]() ,弹簧的长度为
,弹簧的长度为![]() ,根据上表写出
,根据上表写出![]() 与x的关系式;
与x的关系式;
(3)当物体的质量为![]() 时,求弹簧的长度.
时,求弹簧的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并回答问题:
我们知道,乘法公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,如:![]() ,就可以用图1或图2等图形的面积表示.
,就可以用图1或图2等图形的面积表示.
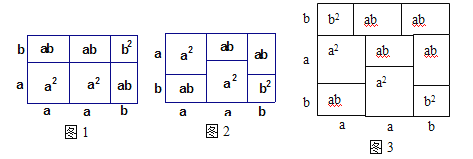
(1)请写出图3所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示:![]() ;
;
(3)请仿照上述方法另写一个含有![]() ,
,![]() 的代数恒等式,并画出与它对应的几何图形.
的代数恒等式,并画出与它对应的几何图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=![]() (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.

(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,BC=AC=3,点D是BC边上一点,∠DAC=30°,点E是AD边上一点,CE绕点C逆时针旋转90°得到CF,连接DF,DF的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com