
【题目】某公司员工分别住在A、B、C、D四个住宅区,A区有20人,B区有15人,C区有5人,D区有30人,四个区在同一条直线上,位置如图所示.该公司的接送车打算在此间设立一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设置在( )
![]()
A. D区 B. A区 C. AB两区之间 D. BC两区之间
【答案】D
【解析】
根据题意分别计算停靠点分别在各点时员工步行的路程和,选择最小的即可解答.
解:∵当停靠点在D区时,所有员工步行到停靠点路程和是:20×800+15×400+5×200=23000m;
当停靠点在A区时,所有员工步行到停靠点路程和是:15×400+5×600+30×800=33000m;
当停靠点在AB两区之间时,设距离B区x米,所有员工步行到停靠点路程和是:20×(400-x)+15x+5×(200+x)+30×(400+x)=(30x+21000)m;
当停靠点在BC两区之间时,设距离B区x米,所有员工步行到停靠点路程和是:20×(400+x)+15x+5×(200-x)+30×(400-x)=21000m.
∴当停靠点在BC两区之间时,所有员工步行到停靠点路程和最小,那么停靠点的位置应该在BC两区之间.
故选:D.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.
(1)求:抛物线的函数表达式;
(2)求:抛物线与y轴的交点C的坐标及其对称轴
(3)若抛物线对称轴上有一点P,使△COA∽△APB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是1.50元/支,但甲、乙两商店的优惠条件有所不同.甲商店:若购买不超过10支,则按标价付款;若一次性购10支以上,则超过10支的部分按标价的60%付款.乙商店:按标价的80%付款.在水性笔的质量等各种因素相同的条件下.
(1)设小明要购买的该品牌水笔数是![]() (
(![]() >10)支,请用含
>10)支,请用含![]() 的代数式分别表示在甲、乙两个商店购买该品牌水性笔的费用.
的代数式分别表示在甲、乙两个商店购买该品牌水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)数轴上有理数﹣10与﹣5对应的两点之间的距离等于 ;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为 ;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于 ;
联系拓广:
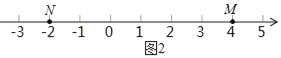
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择 题.
A.①若点P在点M,N两点之间,则|PM|+|PN|= ;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|= ;
若|x+2|+|x﹣4|═10,则x= ;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
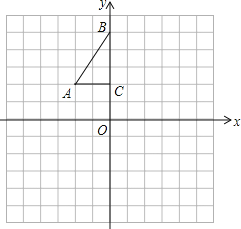
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(-2,2),B(0,5),C(0,2).
(1)画△![]() ,使它与△ABC关于点C成中心对称;
,使它与△ABC关于点C成中心对称;
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),画出平移后对应的![]() ;
;
(3)若将![]() 绕某一点旋转可得到
绕某一点旋转可得到![]() ,则旋转中心的坐标为 _____________.
,则旋转中心的坐标为 _____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
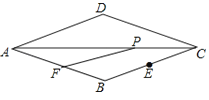
【题目】如图,菱形ABCD中,∠D=135°,AD=6,CE=2![]() ,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值是( )
A. 3 B. 6 C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
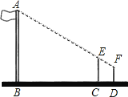
【题目】在一次数学活动课上,小芳到操场上测量旗杆的高度,她的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,利用她所测数据,求旗杆的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com