
����Ŀ���Ķ����ϣ�
С����ѧϰ���θ�ʽ��,����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ��,��![]() .����˼����С������������̽����
.����˼����С������������̽����
��![]() (����a��b��m��n������),����
(����a��b��m��n������),����![]() .
.
��![]() .����С�����ҵ���һ�ְ�����
.����С�����ҵ���һ�ְ�����![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺��a,b,m,n��Ϊ��������
(1)![]() ���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a=___��b=___��
���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a=___��b=___��
(2)��a=7,n=1ʱ����գ�7+ ![]() =�� +
=�� +![]() ��2
��2
(3)��![]() ����a��ֵ.
����a��ֵ.
���𰸡���1��m2+3n2,2mn��2��4,2 (3)28��12
��������
��1��������ȫƽ����ʽչ���õ���m+n![]() ��2=m2+3n2+2
��2=m2+3n2+2![]() mn���Ӷ�����m��n��ʾa��b��
mn���Ӷ�����m��n��ʾa��b��
��2�ɣ�1����֪��n=1����a=m2+3n2=7���ó�m��ֵ���Ӷ��õ�b��ֵ��Ȼ����ռ�����
��3������a=m2+3n2��2mn=6��a��m��n��Ϊ����������ȷ��m��n��ֵ��Ȼ������Ӧ��a��ֵ��
��1����m+n![]() ��2=m2+3n2+2
��2=m2+3n2+2![]() mn����a=m2+3n2��b=2mn��
mn����a=m2+3n2��b=2mn��
��2���ɣ�1����֪��n=1����a=m2+3n2=7�������m=2��������ȥ������m=2��n=1����b=2mn =4����7+4![]() =��2+
=��2+![]() ��2��
��2��
��3��a=m2+3n2��2mn=6��
��a��m��n������������m=3��n=1��m=1��n=3��
����m=3��n=1ʱ��a=9+3=12��
����m=1��n=3ʱ��a=1+3��9=28��
��a��ֵΪ28��12��


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺̽������y��|x|��2��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y��|x|��2��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1���ں���y��|x|��2�У��Ա���x����������ʵ����
��2�������y��x�ļ����Ӧֵ
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | 1 | 0 | ��1 | ��2 | ��1 | 0 | m | �� |
��m���ڶ��٣�
����A��n��2018����B��2020��2018��Ϊ�ú���ͼ���ϲ�ͬ�����㣬��n���ڶ��٣�
��3����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣬����������ĵ㻭���ú�����ͼ���ݺ���ͼ��ɵã��ú�������СֵΪ���٣��ú���ͼ����x��Χ�ɵļ���ͼ�ε�������ڶ��٣�
��4����ֱ֪��y1��![]() x��
x��![]() �뺯��y��|x|��2��ͼ����C��D���㣬��y1��yʱ����ȷ��x��ȡֵ��Χ��
�뺯��y��|x|��2��ͼ����C��D���㣬��y1��yʱ����ȷ��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����С�����о���ѧ���⣺��֪AB��CD��AB��CD����������P��̽����P���C��������ϵ��

���֣�����ͼ�У�����APC=��A+��C����ͼ
С��������֤���ģ�����P��PQ��AB
���APQ=��A(_ __)
��PQ��AB,AB��CD.
��PQ��CD(__ _)
���CPQ=��C
���APQ+��CPQ=��A+��C
����APC=��A+��C
(1)ΪС����֤���������������ݣ�
(2)Ӧ�ã�������ͼ�У���P���A����C��������ϵΪ__ _��
������ͼ��,����A=30![]() ����C=70
����C=70![]() �����P�Ķ���Ϊ__ _��
�����P�Ķ���Ϊ__ _��
(3)��չ������ͼ�У�̽����P���A,��C��������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
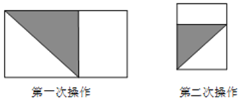
����Ŀ������Ϊ1����Ϊ![]() �ij�����ֽƬ
�ij�����ֽƬ![]() ��ͼ������һ�£�����һ���߳����ڳ����εĿ��ȵ�������
��ͼ������һ�£�����һ���߳����ڳ����εĿ��ȵ�������![]() ��Ϊ��һ�β���
��Ϊ��һ�β���![]() ���ٰ�ʣ�µij�������ͼ������һ�£�����һ���߳����ڴ�ʱ�����ο��ȵ�������
���ٰ�ʣ�µij�������ͼ������һ�£�����һ���߳����ڴ�ʱ�����ο��ȵ�������![]() ��Ϊ�ڶ��β���
��Ϊ�ڶ��β���![]() ����Щ����������ȥ�����ڵ�
����Щ����������ȥ�����ڵ�![]() �β�����ʣ�µij�����Ϊ�����Σ��������ֹ��
�β�����ʣ�µij�����Ϊ�����Σ��������ֹ��
![]() ��һ�β�����ʣ�µij��������߳��ֱ�Ϊ______�� ��
��һ�β�����ʣ�µij��������߳��ֱ�Ϊ______�� ��![]() �ú�
�ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]()
![]() ���ڶ��β�����ʣ�µij�����ǡ���������Σ�����
���ڶ��β�����ʣ�µij�����ǡ���������Σ�����![]() ��ֵ��д�������̣�
��ֵ��д�������̣�
![]() �������β�����ʣ�µij�����ǡ���������Σ�����ͼ�Σ�����
�������β�����ʣ�µij�����ǡ���������Σ�����ͼ�Σ�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
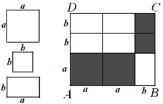
����Ŀ�������ɿ�����ͼ��ʾ�������λ���ֽƬƴ��ͼ��1����ͼ��2��
��1����ͼ��1������AD=7��AB=8����![]() ��
��![]() ��ֵ��
��ֵ��
��2����ͼ��1������������ABCD�����Ϊ35��������Ӱ���ֵ����Ϊ20������ABCD���ܳ���
ͼ��1��
��3����ͼ��2������AD�ij���Ϊ5��AB�ij���Ϊ![]() ��
��
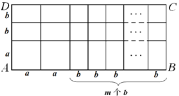
ͼ��2��
�ٵ�![]() =________��
=________��![]() =_________ʱ��
=_________ʱ��![]() ��
��![]() ��ֵ�������飻
��ֵ�������飻
�ڵ�![]() ________��
________��![]() _________ʱ��
_________ʱ��![]() ��
��![]() ��ֵ�����ڣ�
��ֵ�����ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����ֽƬOABC����ƽ��ֱ������ϵxoy�У�ʹOA��OC�ֱ�����x�ᡢy���ϣ��ֽ�ֽƬOABC��OB�۵����۵����A���ڵ�A'��λ�ã���OA=1��OB=2�����A'������Ϊ�� ��
A.![]()
B.![]()
C.�� ![]() ��
��
D.�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ��������O����AD�Ĵ��߽�����AC�ڵ�C��OC��ԲO���ڵ�E������BE��DE��
��1����Բ�İ뾶��3����EBA��30�ȣ���AD�ij��ȣ�
��2����֤����BED=��C��
��3����OA=5��AD=8��������AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y= ![]() ��˫����y=
��˫����y= ![]() ��k��0��x��0�����ڵ�A����ֱ��y=
��k��0��x��0�����ڵ�A����ֱ��y= ![]() ����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����y=
����ƽ��4����λ���Ⱥ���y�ύ�ڵ�C����˫����y= ![]() ��k��0��x��0�����ڵ�B����OA=3BC����k��ֵΪ�� ��
��k��0��x��0�����ڵ�B����OA=3BC����k��ֵΪ�� ��
A.3
B.6
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com