【题目】如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形.若OA1=1，则△A6B6A7的边长为（ ）
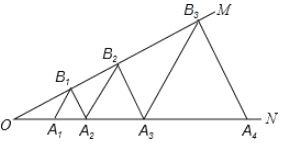
A.32B.24C.16D.8
【答案】A
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及A2B2=2B1A2，得出A3B3=4B1A2=4，A4B4=8B1A2=8，A5B5=16B1A2…进而得出答案．
解：∵△A1B1A2是等边三角形，
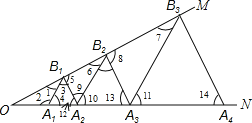
∴A1B1=A2B1，∠3=∠4=∠12=60°，
∴∠2=120°，
∵∠MON=30°，
∴∠1=180°-120°-30°=30°，
又∵∠3=60°，
∴∠5=180°-60°-30°=90°，
∵∠MON=∠1=30°，
∴OA1=A1B1=1，
∴A2B1=1，
∵△A2B2A3、△A3B3A4是等边三角形，
∴∠11=∠10=60°，∠13=60°，
∵∠4=∠12=60°，
∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，
∴∠1=∠6=∠7=30°，∠5=∠8=90°，
∴A2B2=2B1A2，B3A3=2B2A3，
∴A3B3=4B1A2=4，
A4B4=8B1A2=8，
A5B5=16B1A2=16，
以此类推：A6B6=32B1A2=32．
故选A.
科目：初中数学 来源： 题型：
【题目】如图,已知A(3，0),B(0，-1)，连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1，求C点坐标；
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A是反比例函数y＝
在第一象限图象上一点，连接OA，过点A作AB∥x轴（点B在点A右侧），连接OB，若OB平分∠AOX，且点B的坐标是（8，4），则k的值是（ ）
A.6B.8C.12D.16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有甲乙两名采购员去同一家饲料公司分别购买两次饲料，两次购买饲料价格分别为m元/千克和n元/千克，且m≠n，两名采购员的采购方式也不同，其中甲每次购买1000千克，乙每次用去800元，而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少？(用字母m、n表示)
(2)谁的购货方式更合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
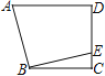
【题目】如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝CD＝8，过点B作EB⊥AB，交CD于点E．若DE＝6，则AD的长为___________.
查看答案和解析>>
科目：初中数学 来源： 题型：
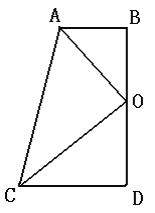
【题目】如图，在四边形ABDC中，∠D=∠B=90°，点O为BD的中点，且AO平分∠BAC.
（1）求证：CO平分∠ACD;
（2）求证：OA⊥OC;
（3）求证：AB+CD=AC.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题：①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等．其中正确的是（ ）
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中A（a,0），B（0，b），且a,b满足
.
(1) (2)
（1）A、B坐标分别为A( ) 、B( ).
（2）P为x轴上一点，C为AB中点，∠APC=∠PBO,求AP的长.
（3）如图2，点E为第一象限一点，AE=AB，以AE为斜边构造等腰直角△AFE，连BE，连接OF并延长交BE于点G，求证：BG=EG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
