
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
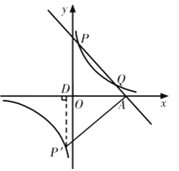
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.

【答案】(1)y=﹣2x+9;(2)(-![]() ,﹣8);(3)
,﹣8);(3)![]()
【解析】试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,∴把点P(![]() ,8)代入
,8)代入![]() 可得:k2=4,∴反比例函数的表达式为
可得:k2=4,∴反比例函数的表达式为![]() ,∴Q (4,1).
,∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入
,8),Q (4,1)分别代入![]() 中,得:
中,得: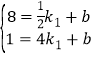 ,解得:
,解得:![]() ,∴一次函数的表达式为y=﹣2x+9;
,∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(![]() ,﹣8),∴OD=
,﹣8),∴OD=![]() ,P′D=8,∵点A在y=﹣2x+9的图象上,∴点A(
,P′D=8,∵点A在y=﹣2x+9的图象上,∴点A(![]() ,0),即OA=
,0),即OA=![]() ,∴DA=5,∴P′A=
,∴DA=5,∴P′A=![]() =
=![]() ,∴sin∠P′AD=
,∴sin∠P′AD=![]() =
=![]() ,∴sin∠P′AO=
,∴sin∠P′AO=![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,O是直线AB上一点,OD是∠AOC的平分线,∠COD与∠COE互余
求证:∠AOE与∠COE互补.

请将下面的证明过程补充完整:
证明:∵O是直线AB上一点
∴∠AOB=180°
∵∠COD与∠COE互余
∴∠COD+∠COE=90°
∴∠AOD+∠BOE=_________°
∵OD是∠AOC的平分线
∴∠AOD=∠________(理由:_______________)
∴∠BOE=∠COE(理由:________________)
∵∠AOE+∠BOE=180°
∴∠AOE+∠COE=180°
∴∠AOE与∠COE互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转( )圈.
A. 4 B. 3 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,将过点
,将过点![]() 的直线
的直线![]() 绕点
绕点![]() 旋转,交射线
旋转,交射线![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .
.
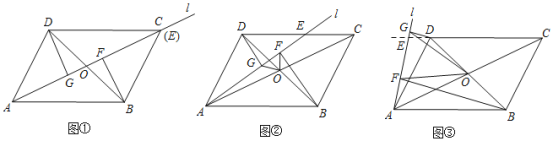
![]() 如图
如图![]() 当点
当点![]() 与点
与点![]() 重合时,请直接写出线段
重合时,请直接写出线段![]() 的数量关系;
的数量关系;
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 上时,
上时,![]() 与
与![]() 有什么数量关系?请说明你的结论;
有什么数量关系?请说明你的结论;
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 有什么数量关系?请说明你的结论.
有什么数量关系?请说明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
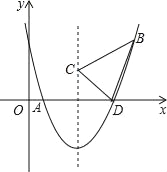
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
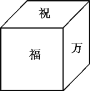
【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
A. 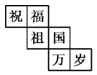 B.
B. 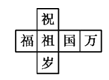 C.
C. 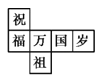 D.
D. 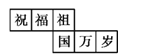
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com