
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
计算
(1)1022;(2)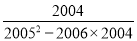 ;(3)(3x2)2•(﹣4y3)÷(6xy)2 ;
;(3)(3x2)2•(﹣4y3)÷(6xy)2 ;
(4)(2a+b﹣4)(2a+b+4);(5)a2(a+b)(a-b)+a2b2 ;(6)(2﹣π)0+(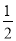 )﹣2+(﹣
)﹣2+(﹣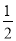 )2016×22017
)2016×22017
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
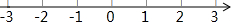 解不等式组,并把解集表示在数轴上.
解不等式组,并把解集表示在数轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
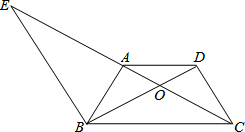 如图,等腰梯形ABCD中,AD∥BC,对角线AC、BD交于点O,过点B作BE∥CD交CA的延长线于E.
如图,等腰梯形ABCD中,AD∥BC,对角线AC、BD交于点O,过点B作BE∥CD交CA的延长线于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com