
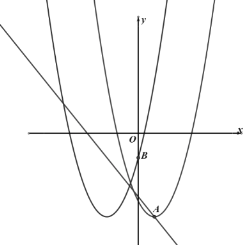
【题目】已知抛物线![]() :
:![]() ,其中
,其中![]() .
.
(1)以下结论正确的序号有_________;
①抛物线的对称轴是直线![]() ; ②抛物线经过定点
; ②抛物线经过定点![]() ,
,![]() ;
;
③函数![]() 随着
随着![]() 的增大而减小; ④抛物线的顶点坐标为
的增大而减小; ④抛物线的顶点坐标为![]() .
.
(2)将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() .
.
①若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的解析式;
的解析式;
②抛物线![]() 顶点的纵坐标
顶点的纵坐标![]() 与横坐标
与横坐标![]() 之间存在一个函数关系,求这个函数关系式,并写出
之间存在一个函数关系,求这个函数关系式,并写出![]() 的取值范围;
的取值范围;
③若抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,求
,求![]() 间的最小距离.
间的最小距离.
【答案】(1)①②④;(2)①y=4x2+16x-5,②![]()
![]() ,③
,③![]() 之间的最小距离是
之间的最小距离是![]() .
.
【解析】
(1)①将抛物线化为顶点式即可得出结果;②将![]() 变形为
变形为![]() ,令x2+4x=0,从而可得出结果;③根据k>0以及抛物线的对称轴可得出结果;④根据顶点式可得出结果;
,令x2+4x=0,从而可得出结果;③根据k>0以及抛物线的对称轴可得出结果;④根据顶点式可得出结果;
(2)①根据平移的性质可得抛物线L1的对称轴为直线![]() ,再根据两条抛物线关于y轴对称可得出关于k的方程,解得k即可得出结果;
,再根据两条抛物线关于y轴对称可得出关于k的方程,解得k即可得出结果;
②根据平移的性质可得出抛物线L1的解析式为![]() ,其顶点坐标为
,其顶点坐标为![]() ,再根据
,再根据![]() ,
,![]() ,消去k可得出x,y之间的函数关系式,同时结合k>0,可得出x的取值范围;
,消去k可得出x,y之间的函数关系式,同时结合k>0,可得出x的取值范围;
③设点![]() 的坐标为
的坐标为![]() ,根据两点间的距离公式,可用含a的式子表示出AB的长,结合二次函数的性质可得出AB的最小值.
,根据两点间的距离公式,可用含a的式子表示出AB的长,结合二次函数的性质可得出AB的最小值.
解:(1)∵![]() ,
,
∴抛物线的对称轴是直线x=-2,顶点坐标为(-2,-4k-5),
故①、④正确;
将![]() 变形为
变形为![]() ,
,
令x2+4x=0,解得x=0或x=-4,
∴抛物线经过定点(0,-5),(-4,-5),
故②正确;
∵k>0,抛物线的对称轴为直线x=-2,
∴当x<-2时,y随x的增大而减小;当x>-2时,y随x的增大而增大,
故③错误;
故答案为:①②④;
(2)①∵将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,抛物线
,抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,∴抛物线
,∴抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,
,
∵抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,
轴对称,
∴![]() ,∴
,∴![]() ,
,
∴平移后的抛物线![]() 的解析式为y=4x2+16x-5;
的解析式为y=4x2+16x-5;
②∵![]() ,
,
∴抛物线![]() :
:![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∴抛物线L向右平移k个单位后的抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
![]() ;
;
③![]() 中令x=0,则y=-5,∴
中令x=0,则y=-5,∴![]() .
.
点![]() 是直线
是直线![]() 上的动点,设点
上的动点,设点![]() 的坐标为
的坐标为![]() ,
,
则 ,
,
∴当a=![]() 时,线段
时,线段![]() 有最小值,最小值是
有最小值,最小值是![]() .
.
即![]() 之间的最小距离是
之间的最小距离是![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
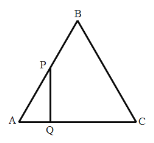
【题目】如图等边![]() 的边长为
的边长为![]() ,点
,点![]() ,点
,点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿
沿![]() 以
以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 沿
沿![]() 以
以![]() 的速度也向点
的速度也向点![]() 运动,直到到达点
运动,直到到达点![]() 时两点都停止运动,若
时两点都停止运动,若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则下列最能反映
,则下列最能反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A.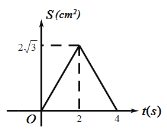 B.
B.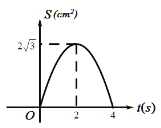
C.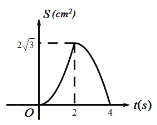 D.
D.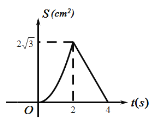
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 将
将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() 连接
连接![]() .
.
(1)若![]() 求抛物线的解析式.
求抛物线的解析式.
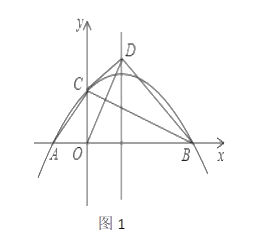
(2)如图1,设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,![]() 若
若![]() 点是半径为
点是半径为![]() 的
的![]() 上一动点,连接
上一动点,连接![]() 当点
当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最大,请求出这个最大值,并说明理由.
的值最大,请求出这个最大值,并说明理由.
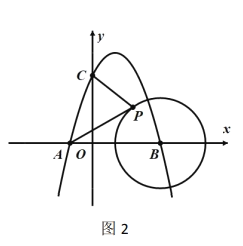
查看答案和解析>>
科目:初中数学 来源: 题型:
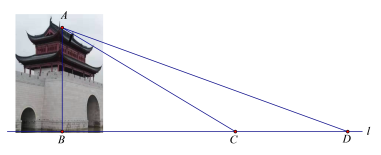
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______________________;
(Ⅱ)解不等式②,得____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港口![]() 、
、![]() 、
、![]() 依次在同一条直线上,甲、乙两艘船同时分别从
依次在同一条直线上,甲、乙两艘船同时分别从![]() 、
、![]() 两港出发,沿该直线匀速行驶向
两港出发,沿该直线匀速行驶向![]() 港,甲、乙两船与
港,甲、乙两船与![]() 港之间的距离
港之间的距离![]() (海里)与行驶时间
(海里)与行驶时间![]() (小时)之间的函数关系如图所示,则下列说法:①甲船的平均速度为60海里/小时;②乙船的平均速度为30海里/小时;③甲、乙两船在途中相遇两次;④
(小时)之间的函数关系如图所示,则下列说法:①甲船的平均速度为60海里/小时;②乙船的平均速度为30海里/小时;③甲、乙两船在途中相遇两次;④![]() 、
、![]() 两港之间的距离为30海里;⑤
两港之间的距离为30海里;⑤![]() 、
、![]() 两港之间的距离为90海里.其中正确的有( )
两港之间的距离为90海里.其中正确的有( )
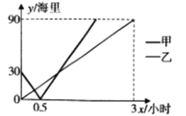
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
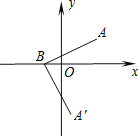
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
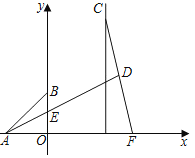
【题目】如图,A、B两点的坐标分别为(﹣4,0),(0,4),C、F分别是直线x=6和x轴上的动点,CF=12,D是CF的中点,连接AD交y轴与点E,△ABE面积的最小值为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com