
【题目】港口![]() 、
、![]() 、
、![]() 依次在同一条直线上,甲、乙两艘船同时分别从
依次在同一条直线上,甲、乙两艘船同时分别从![]() 、
、![]() 两港出发,沿该直线匀速行驶向
两港出发,沿该直线匀速行驶向![]() 港,甲、乙两船与
港,甲、乙两船与![]() 港之间的距离
港之间的距离![]() (海里)与行驶时间
(海里)与行驶时间![]() (小时)之间的函数关系如图所示,则下列说法:①甲船的平均速度为60海里/小时;②乙船的平均速度为30海里/小时;③甲、乙两船在途中相遇两次;④
(小时)之间的函数关系如图所示,则下列说法:①甲船的平均速度为60海里/小时;②乙船的平均速度为30海里/小时;③甲、乙两船在途中相遇两次;④![]() 、
、![]() 两港之间的距离为30海里;⑤
两港之间的距离为30海里;⑤![]() 、
、![]() 两港之间的距离为90海里.其中正确的有( )
两港之间的距离为90海里.其中正确的有( )
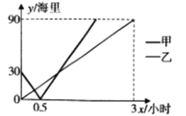
A.1个B.2个C.3个D.4个
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,沿对角线BD翻折△BCD,点E是点C的落点,BE交AD于点F,若CD=4,EF=3,则BD的长为( )
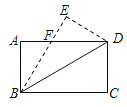
A.5B.5![]() C.4
C.4![]() D.10
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其中
,其中![]() .
.
(1)以下结论正确的序号有_________;
①抛物线的对称轴是直线![]() ; ②抛物线经过定点
; ②抛物线经过定点![]() ,
,![]() ;
;
③函数![]() 随着
随着![]() 的增大而减小; ④抛物线的顶点坐标为
的增大而减小; ④抛物线的顶点坐标为![]() .
.
(2)将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() .
.
①若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的解析式;
的解析式;
②抛物线![]() 顶点的纵坐标
顶点的纵坐标![]() 与横坐标
与横坐标![]() 之间存在一个函数关系,求这个函数关系式,并写出
之间存在一个函数关系,求这个函数关系式,并写出![]() 的取值范围;
的取值范围;
③若抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,求
,求![]() 间的最小距离.
间的最小距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于G,过C点的切线与射线
于G,过C点的切线与射线![]() 相交于点E,直线
相交于点E,直线![]() 与
与![]() 交于点H,
交于点H,![]() ,
,![]() .
.

(Ⅰ)求![]() 的半径;
的半径;
(Ⅱ)将射线![]() 绕D点逆时针旋转,得射线
绕D点逆时针旋转,得射线![]() (如图2),
(如图2),![]() 与
与![]() 交于点M,与
交于点M,与![]() 及切线
及切线![]() 分别相交于点N,F,当
分别相交于点N,F,当![]() 时,求切线
时,求切线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
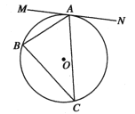
【题目】已知,![]() 内接于
内接于![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,点![]() 为
为![]() 的中点,射线
的中点,射线![]() 交
交![]() 于点
于点![]() ,交优弧
,交优弧![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图,在(2)的条件下,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
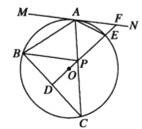
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
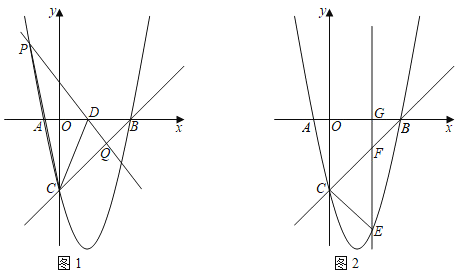
【题目】抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.
(1)试求二次函数及一次函数的解析式;
(2)如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD,求点P的坐标;
(3)如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+![]() CF的值最大时,求点E的坐标.
CF的值最大时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,毛毛对该班同学参加锻炼的情况进行了统计(每人只能选其中一项),并绘制了如图两个统计图,请根据图中提供的信息解答下列问题:
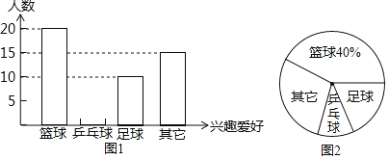
(1)毛毛这次一共调查了多少名学生?
(2)补全条形统计图,并求出扇形统计图中“足球”所在扇形的圆心角度数;
(3)若该校有1800名学生,请估计该校喜欢乒乓球的学生约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com