
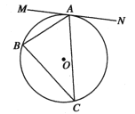
【题目】已知,![]() 内接于
内接于![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() .
.
(1)如图,求证:![]() ;
;
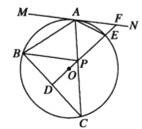
(2)如图,点![]() 为
为![]() 的中点,射线
的中点,射线![]() 交
交![]() 于点
于点![]() ,交优弧
,交优弧![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;

(3)如图,在(2)的条件下,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析;(2)见解析;(3)![]() 的半径为
的半径为![]()
【解析】
(1)如下图,根据切线和直径所对圆周角为90°得到![]() 和
和![]() ,通过角度转化可证
,通过角度转化可证![]() ;
;
(2)如下图,设![]() ,推导可得出
,推导可得出![]() ,
,![]() ,
,![]() ,从而证
,从而证![]() ;
;
(3)如下图,设![]() ,则
,则![]() ,先证
,先证![]() ,从而得出
,从而得出![]() ,最后可利用
,最后可利用![]() 的关系得出k的值和
的关系得出k的值和![]() 的半径.
的半径.
(1)证明:过点![]() 作直径
作直径![]() ,连接
,连接![]() .
.
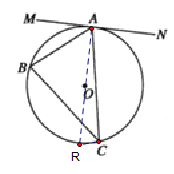
∵![]() 是
是![]() 直径,∴
直径,∴![]() .∴
.∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .
.
∵![]() 是
是![]() 切线,∴
切线,∴![]() .
.
∴![]() .∴
.∴![]() .
.
(2)证明:延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,

设![]() .∵
.∵![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() .
.
∵点![]() 为
为![]() 中点,
中点,![]() 不是直径,
不是直径,
∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴AG∥BC.∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]() .
.
(3)解:如图,连接![]() ,设
,设![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]()
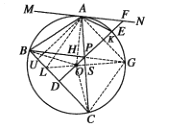
由(2)知![]() 于点
于点![]() ,且
,且![]() ,
,
∴![]() .
.
∵BP∥MN,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() 垂直平分
垂直平分![]() .∴
.∴![]() .
.
∴![]() .
.
∴设![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() ,
,![]() .
.
∴![]() .∴
.∴![]() .
.
∵![]() =
=![]() ,∴
,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() 垂直平分
垂直平分![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() 垂直平分
垂直平分![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴![]() ,即
,即![]() 的半径为
的半径为![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,将这些学生的测试成绩(x)分为四个等级:优秀![]() ;良好
;良好![]() ;及格
;及格![]() ;不及格
;不及格![]() ,并绘制成以下两幅统计图.
,并绘制成以下两幅统计图.
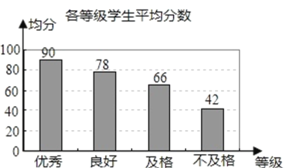

根据以上信息,解答下列问题:
(1)在抽取的学生中不及格人数所占的百分比是______;
(2)计算所抽取学生测试成绩的平均分;
(3)若不及格学生的人数为2人,请估算出该校九年级学生中优秀等级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
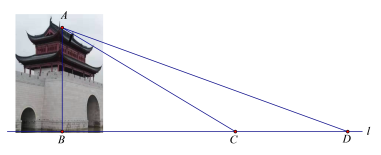
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______________________;
(Ⅱ)解不等式②,得____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港口![]() 、
、![]() 、
、![]() 依次在同一条直线上,甲、乙两艘船同时分别从
依次在同一条直线上,甲、乙两艘船同时分别从![]() 、
、![]() 两港出发,沿该直线匀速行驶向
两港出发,沿该直线匀速行驶向![]() 港,甲、乙两船与
港,甲、乙两船与![]() 港之间的距离
港之间的距离![]() (海里)与行驶时间
(海里)与行驶时间![]() (小时)之间的函数关系如图所示,则下列说法:①甲船的平均速度为60海里/小时;②乙船的平均速度为30海里/小时;③甲、乙两船在途中相遇两次;④
(小时)之间的函数关系如图所示,则下列说法:①甲船的平均速度为60海里/小时;②乙船的平均速度为30海里/小时;③甲、乙两船在途中相遇两次;④![]() 、
、![]() 两港之间的距离为30海里;⑤
两港之间的距离为30海里;⑤![]() 、
、![]() 两港之间的距离为90海里.其中正确的有( )
两港之间的距离为90海里.其中正确的有( )
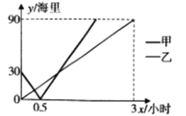
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如图不完整统计图.请结合图中信息,解决下列问题.
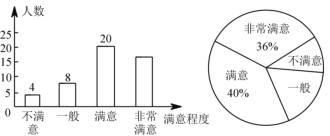
(1)此次调查中接受调查的人数为______人,其中“非常满意”的人数为______人;“一般”部分所在扇形统计图的圆心角度数为_______.
(2)兴趣小组准备从“不满意”的![]() 位群众中随机选择
位群众中随机选择![]() 位进行回访,已知这
位进行回访,已知这![]() 位群众中有
位群众中有![]() 位来自甲片区,另
位来自甲片区,另![]() 位来自乙片区,请用画树状图或列表的方法求出选择的群众都来自甲片区的概率.
位来自乙片区,请用画树状图或列表的方法求出选择的群众都来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为_____.
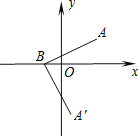
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=![]() m与y轴交于点C,与x轴交于点A和点B(其中点A在y轴左侧,点B在y轴右侧).
m与y轴交于点C,与x轴交于点A和点B(其中点A在y轴左侧,点B在y轴右侧).
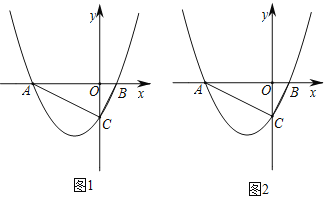
(1)若抛物线y=![]() m的对称轴为直线x=1,求抛物线的解析式;
m的对称轴为直线x=1,求抛物线的解析式;
(2)如图1,∠ACB=90°,点P是抛物线y=![]() m上的一点,若S△BCP=
m上的一点,若S△BCP=![]() ,求点P的坐标;
,求点P的坐标;
(3)如图2,过点A作AD∥BC交抛物线于点D,若点D的纵坐标为﹣![]() m,求直线AD的解析式.
m,求直线AD的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com