
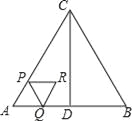
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=4cm��CD��AB�ڵ�D������P�ӵ�A��������AC��2cm/s���ٶ����յ�C�˶�������P��������P��PQ��BC������AD��DC�ڵ�Q����PQΪ�����ȱ�������PQR�����ı���APRQ����ACD�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����
��1������Q���߶�AD��ʱ���ú�t�Ĵ���ʽ��ʾQR�ij���
��2�����R�˶���·�̳���
��3������Q���߶�AD��ʱ����S��t֮��ĺ�����ϵʽ��
��4��ֱ��д���Ե�B��Q��RΪ�������������ֱ��������ʱt��ֵ��
���𰸡�(1) 2t��(2) 2![]() +2��(3) ��0��t��
+2��(3) ��0��t��![]() ʱ��S=2
ʱ��S=2![]() t2����
t2����![]() ��t��1ʱ��S=-
��t��1ʱ��S=-![]() t2+6
t2+6![]() t-2
t-2![]() ��(4) t=
��(4) t=![]() ��t=
��t=![]()
�������������������1����֤��APQ�ǵȱ������Σ����ɵõ�QR=PQ=AP=2t��
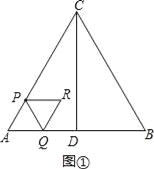
��2������A��AG��BC�ڵ�G����ͼ�����õ�R�˶���·�̳���AG+CG��ֻ�����AG��CG�Ϳɽ�����⣻
��3���ı���APRQ����ACD�ص�����ͼ�ο��������Σ�Ҳ����������Σ������������ۣ�Ȼ�����ø���Ϳɽ�����⣻
��4������ֱ�Ƕ��㲻ȷ���������������ۣ�ֻ�����QRB=90������RQB=90������������ۣ����ɽ�����⣮
�����������1����ͼ����
�ߡ�ABC�ǵȱ������Σ�
���ACB=��B=60����
��PQ��BC��
���APQ=��ACB=60������AQP=��B=60����
���APQ�ǵȱ������Σ�
��PQ=AP=2t��
�ߡ�PQR�ǵȱ������Σ�
��QR=PQ=2t��
��2������A��AG��BC�ڵ�G����ͼ����
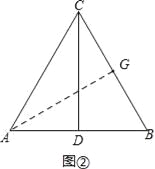
���R�˶���·�̳���AG+CG��
��Rt��AGC����AGC=90����sin60��=![]() ��cos60��=
��cos60��=![]() ��AC=4��
��AC=4��
��AG=2![]() ��CG=2��
��CG=2��
����R�˶���·�̳�2![]() +2��
+2��
��3������0��t��![]() ʱ����ͼ����
ʱ����ͼ����
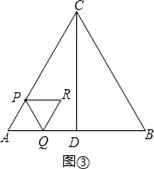
S=S����APRQ=2��S����APQ=2��![]() ����2t��2=2
����2t��2=2![]() t2��
t2��
����![]() ��t��1ʱ����ͼ��
��t��1ʱ����ͼ��
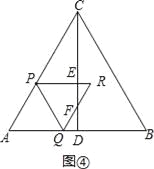
PE=PCsin��PCE=��4��2t����![]() =2��t��
=2��t��
��ER=PR��PE=2t����2��t��=3t��2��
��EF=ERtanR=![]() ��3t��2��
��3t��2��
��S=S����APRQ��S��REF
=2![]() t2��
t2��![]() ��3t��2��2=��
��3t��2��2=��![]() t2+6
t2+6![]() t��2
t��2![]() ��
��
��4��t=![]() ��t=
��t=![]()
��ʾ��������QRB=90��ʱ����ͼ����
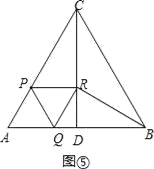
cos��RQB=![]() ��
��
��QB=2QR=2QA��
��AB=3QA=6t=4��
��t=![]() ��
��
������RQB=90��ʱ����ͼ����
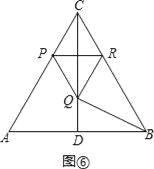
ͬ���ɵ�BC=3RC=3PC=3��4��2t��=4��
��t=![]() ��
��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b�������и�����ʽ��һ���������ǣ� ��
A.a��1��b��1
B.��a����b
C.![]()
D.ac��bc
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��չ�ô�μ���������Ϊ20Ԫ������͵���Ϊ80Ԫ������100����
��1���蹺��������Ϊx��������������������ܷ���Ϊy��Ԫ��������д��y��x�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2�����������������ܷ��ò�����6620Ԫ��������������������������3������ô���ļ��ֹ�����
��3���ӽ�Լ��֧�ĽǶ�����������Ϊ�������ַ��������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒԭ��ÿ���ijɱ���1000Ԫ�������������ν��ͳɱ������ڵijɱ���810Ԫ����ƽ��ÿ�ν��ͳɱ���������
A. 8.5%B. 9%C. 9.5%D. 10%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У���ֵ��ȵ����� ��
A. ����2��3�멁23 B. 23��32
C. ����3��2�멁32 D. ����-2���멁|��2|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD����AD��BC��AC�ǶԽ���������CAD����ACB��������ı�����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У���a��b��cΪ�߳��������β���ֱ�������ε��ǣ� ��
A.a=3��b=4��c=5
B.a=5��b=12��c=13
C.a=1��b=2��c= ![]()
D.a= ![]() ��b=2��c=3
��b=2��c=3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com