练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．下列函数关系中表示一次函数的有（　　）
    ①y=2x+1  ②y=$\frac{2}{x}$  ③y=-3x2+1  ④s=60t  ⑤y=100-25x．
    A．1个B．2个C．3个D．4个

    分析 依据一次函数的定义回答即可．

    解答 解：①是一次函数，②是反比例函数，③二次函数，④一次函数，⑤一次函数．
    故选：C．

    点评 本题主要考查的是一次函数的定义，掌握一次函数的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．小聪用一条长21米的绳子，借助一面墙围，成了如图所示的长方形．
    （1）若长方形的长比宽多9米，求长方形的面积是多少．
    （2）若长方形的长是宽的5倍，此时长、宽各为多少米？
    （3）若长方形的长与宽相等，即围成一个正方形，此时正方形的边长是少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

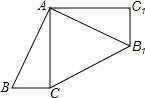    12．如图，∠ACB=90°，把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1，若BC=1，AB=2，则CB1的长度是$\sqrt{7-2\sqrt{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解方程组$\left\{\begin{array}{l}{3x+4y=3①}\\{2x-y=5②}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．已知等边三角形的边长为a，则它边上的高、面积分别是（　　）
    A．$\frac{a}{2}$，$\frac{{a}^{2}}{4}$B．$\frac{\sqrt{3}a}{2}$，$\frac{{a}^{2}}{4}$C．$\frac{\sqrt{3}a}{2}$，$\frac{\sqrt{3}{a}^{2}}{4}$D．$\frac{3a}{4}$，$\frac{\sqrt{3}{a}^{2}}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知，AD是△ABC中BC边上的中线，若AB=3，AD=2，则AC的取值范围是1＜AC＜7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知|a|=3，b2=4，|a+b|=a+b，求a-3b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．为了发展农村经济，政府决定从2011年起，鼓励农民种植果树．并出台了一项奖励措施：在种植过程中，每一年新增面积达到10亩的农户，可得到1500元生活补贴，且每超出一亩，政府还给予m元的奖励，另外种植果树后的土地从下一年起，果实即可出售，且平均每亩可获得200元的收入．如表是某农户头两年种植果树每年获得总收入情况：
    年份新增亩数总收入
    2011202400元
    2012266940元
    （提示：年总收入=生活补贴+政府奖励+出售果实收入）
    （1）根据以上提供的信息求m的值．
    （2）如果该农户在2013年新增30亩，那么他2013年的年总收入是多少？
    （3）现政府规定若收入超过1万元，则取消生活补助，并且超出部分需缴纳10%的个人所得税，从2012年起，如果该农户每年增加的新增面积均能按相同的亩数增长，那么2014年该农户总收入是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

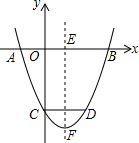    11．如图，抛物线y=x2-mx+n经过点A（-1，0），与x轴的另一个交点是B（B在A的右侧），与y轴交于点C，抛物线的对称轴EF交x轴于点E，点C关于EF的对称点是点D．
    （1）n=-m-1（用含m的代数式表示）．
    （2）当点E是OA中点时，求该抛物线对应的函数关系式．
    （3）当以点A，C，D，E为顶点的四边形是平行四边形时，求m的值．
    （4）连结AC、CE，当△ACE的面积是$\frac{1}{2}$时，直接写出m的值．

    查看答案和解析>>

    同步练习册答案