
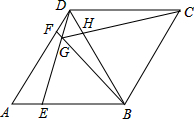
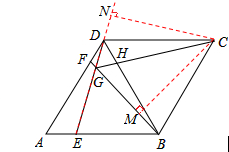
 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |


科目:初中数学 来源: 题型:
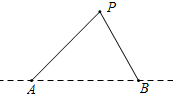 国外船只,除特许外,不得进入我国海洋100海里以内区域.如图,设A,B是我们观察站A和B之间为150海里,海岸线是过A,B的一条直线,一外国船只在P点,在A点测到∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告?
国外船只,除特许外,不得进入我国海洋100海里以内区域.如图,设A,B是我们观察站A和B之间为150海里,海岸线是过A,B的一条直线,一外国船只在P点,在A点测到∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、l个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1个 | B、2 | C、3个 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 22 |
| 7 |
| 1 |
| 3 |
| π |
| 3 |
| •• |
| 31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com