
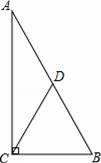
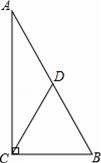
如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD=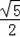
 ,如果Rt△ABC的面积为1,则它的周长为( )
,如果Rt△ABC的面积为1,则它的周长为( )

A.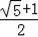
 B.
B.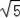
 +1 C.
+1 C.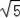
 +2 D.
+2 D.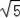
 +3
+3
D【考点】勾股定理;直角三角形斜边上的中线.
【专题】计算题.
【分析】根据“直角三角形斜边上的中线等于斜边的一半求得AB=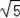
 ;然后利用勾股定理、三角形的面积求得(AC+BC)的值,则易求该三角形的周长.
;然后利用勾股定理、三角形的面积求得(AC+BC)的值,则易求该三角形的周长.
【解答】解:如图,∵在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD=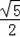
 ,
,
∴AB=2CD=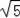
 .
.
∴AC2+BC2=5
又∵Rt△ABC的面积为1,
∴
 AC•BC=1,则AC•BC=2.
AC•BC=1,则AC•BC=2.
∴(AC+BC)2=AC2+BC2+2AC•BC=9,
∴AC+BC=3(舍去负值),
∴AC+BC+AB=3+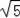
 ,即△ABC的周长是3+
,即△ABC的周长是3+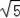
 .
.
故选:D.

【点评】本题考查了勾股定理,直角三角形斜边上的中线.此题借助于完全平方和公式求得(AC+BC)的长度,减少了繁琐的计算.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
有下列命题:
①两直线平行,同旁内角相等;
②面积相等的两个三角形全等;
③有一个角为45°的等腰三角形必为直角三角形;
④直角三角形的两条边长分别为3和4,则斜边长为5或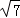 .
.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
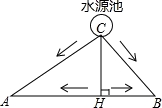
如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
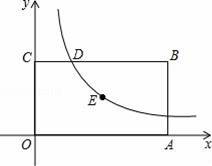
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=
 (x>0)的图象经过矩形的对称中心E,且与边BC交于点D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com