
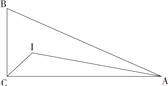
【题目】如图,Rt△ABC中,∠ACB=90°,BC=5,AC=12,I是Rt△ABC的内心,连接CI,AI,则△CIA外接圆的半径为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】过I作ID⊥AC于D,设△CIA的外接圆为⊙O,连接CO,IO,AO.
由勾股定理得到AB的长.由公式直角三角形内切圆半径=(a+b-c)÷2,得到内切圆半径ID的长,由CD=ID,得到CD的长.以C为坐标原点,CA所在直线为x轴,向右为正方向,CB所在直线为y轴,向上为正方向建立直角坐标系,则C(0,0),I(2,2)A(12,0).设O(x,y),由OC=OI=OA,用两点间距离公式列方程组,求解即可得到O的坐标,即可得到结论.
过I作ID⊥AC于D,设△CIA的外接圆为⊙O,连接CO,IO,AO.
∵∠ACB=90°,BC=5,AC=12,∴AB=13.
∵I是Rt△ABC的内心,ID⊥AC,∴ID为内切圆半径,ID=(5+12-13)÷2=2,∴CD=ID=2.以C为坐标原点,CA所在直线为x轴,向右为正方向,CB所在直线为y轴,向上为正方向建立直角坐标系,则C(0,0),I(2,2)A(12,0).设O(x,y).
∵OC=OI=OA,∴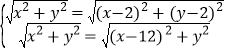 ,解得:
,解得:![]() ,∴O(6,-4),∴△CIA外接圆的半径=CO=
,∴O(6,-4),∴△CIA外接圆的半径=CO=![]() =
=![]() .
.
故选C.



科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有_____________(写出所有正确结论的序号).
①∠N\AF=45°;②当P为 BC中点时,AE为线段NP的中垂线;
③四边形AMCB的面积最大值为10; ④线段AM的最小值为2![]() ;
;
⑤当△ABP≌△ADN时,BP=4![]() -4.
-4.

查看答案和解析>>
科目:初中数学 来源: 题型:
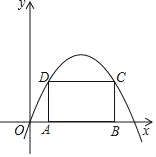
【题目】如图,A,B两点在x轴的正半轴上运动,四边形ABCD是矩形,C,D两点在抛物线y=﹣x2+8x上.
(1)若OA=1,求矩形ABCD的周长;
(2)设OA=m(0<m<4),求出四边形ABCD的周长L关于m的函数表达式;
(3)在(2)的条件下求L的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑期临近,重庆市某中学校为了丰富学生的暑期文化生活,同时帮助孩子融洽亲子关系,增进亲子间的情感交流,计划组织学生去某景区参加为期一周的“亲子一家游”活动. 若报名参加此次活动的学生人数共有56人,其中要求参加的每名学生都至少需要一名家长陪同参加.
(1)假设参加此次活动的家长人数是参加学生人数的2倍少2人,为了此次活动学校专门为每名学生和家长购买一件T恤衫, 家长的T恤衫每购买8件赠送1件学生T恤衫(不足8件不赠送),学生T恤衫每件15元,学校购买服装的费用不超过3401元,请问每件家长T恤衫的价格最高是多少元?
(2)已知该景区的成人票价每张100元,学生票价每张50元,为了支持此次活动,该景区特地推出如下优惠活动:每张成人票价格下调a%,学生票价格下调.![]() a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了
a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
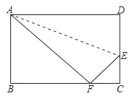
【题目】如图已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
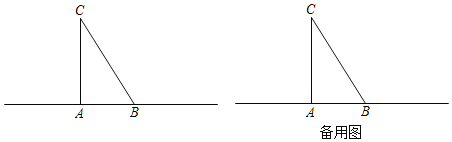
(1)试用直尺和圆规,在直线AB上求作点P,使![]() 为等腰三角形.要求:①保留作图痕迹;②若点P有多解,则应作出所有的点P,并在图中依次标注
为等腰三角形.要求:①保留作图痕迹;②若点P有多解,则应作出所有的点P,并在图中依次标注![]() 、
、![]() 、
、![]() …;
…;
(2)根据(1)求PA的长(所有可能的值).
查看答案和解析>>
科目:初中数学 来源: 题型:
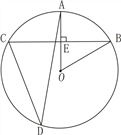
【题目】如图,在⊙O 中,BC是弦,OA⊥BC于点E,D为⊙O上一点,连接AD,CD.
(1)求证:∠AOB=2∠ADC;
(2)若OB⊥CD,CD=8,OE=![]() ,求tan∠ADC.
,求tan∠ADC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 满足
满足![]() .
.
![]()
(1)点![]() 表示的数为 ;点
表示的数为 ;点![]() 表示的数为 ;
表示的数为 ;
(2)甲球从点![]() 处以1个单位长度/秒的速度向左运动;同时乙球从点
处以1个单位长度/秒的速度向左运动;同时乙球从点![]() 处以2个单位/秒的速度也向左运动,设运动的时间为
处以2个单位/秒的速度也向左运动,设运动的时间为![]() (秒),
(秒),
①当![]() 时,甲球到原点的距离为 单位长度;乙球到原点的距离为 单位长度;当
时,甲球到原点的距离为 单位长度;乙球到原点的距离为 单位长度;当![]() 时,甲球到原点的距离为 单位长度;乙球到原点的距离为 单位长度;
时,甲球到原点的距离为 单位长度;乙球到原点的距离为 单位长度;
②试探究:在运动过程中,甲、乙两球到原点的距离可能相等吗?若不能,请说明理由,若能,求出甲、乙两球到原点的距离相等时的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学参加社会实践活动,到“庐江台湾农民创业园”了解大棚蔬菜生长情况.他们分两组对西红柿的长势进行观察测量,分别收集到10株西红柿的高度,记录如下(单位:厘米)
第一组:32 39 45 55 60 54 60 28 56 41
第二组:51 56 44 46 40 53 37 47 50 46
根据以上数据,回答下列问题:
(1)第一组这10株西红柿高度的平均数是 ,中位数是 ,众数是 .
(2)小明同学计算出第一组方差为S12=122.2,请你计算第二组方差,并说明哪一组西红柿长势比较整齐.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com